Numerik Applets

Stabilität und Konvergenz

Bei der numerischen Lösung von Anfangswertaufgaben

$\begin{displaymath} \begin{array}{ll} \dot{x}(t)=f(x(t),t) & t\in[a,b]\\ x(t_0)=x_0 \par \end{array} \end{displaymath}$

können je nach gewähltem Integrationsverfahren gute oder schlechte Approximation der Lösung berechnet werden.

Wir betrachten die Differentialgleichung

$\begin{displaymath}\left(% \begin{array}{c} x_1'(t) \\ x_2'(t) \\ \end{a... ..._1(t)+7x_2(t) \\ -8\lambda x_2(t) \\ \end{array}% \right)\end{displaymath}$

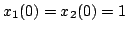mit den Anfangswerten $x_1(0)=x_2(0)=1$ und der exakten Lösung (gelb)

$\begin{equation*} \begin{aligned} x_1(t)&= \frac{e^{\lambda t}(1+\lambda)-e^{... ...bda t}}{\lambda}\\ x_2(t)&=e^{-8\lambda t}\\ \end{aligned} \end{equation*}$

Sie wird mit zwei konsistenten Integrationsverfahren der Ordnung 4 gelöst.

Das erste Verfahren ist das lineare Zweischrittverfahren (rot)

$\displaystyle x_l=x_{l-2}+h(\frac{1}{3}f(x_{l},t_{l})+\frac{4}{3}f(x_{l-1},t_{l-1})+\frac{1}{3}f(x_{l-2},t_{l-2})).$

Das zweite ist das klassische vierstufige Runge-Kutta-Verfahren (blau), dass durch das Butcher-Tableau

$\displaystyle \begin{tabular}{c\vert cccc} 0 & 0 & & & \ \rule{0mm}{5mm} $\f... ...c{1}{6}$ & $\frac{1}{3}$ & $\frac{1}{3}$ & $\frac{1}{6}$ \\ \end{tabular}$

beschrieben wird.

Vergleichen Sie für verschiedene Schrittweiten die exakte Lösung, mit den Näherungslösungen der beiden Verfahren.

Überprüfen Sie das Dahlquistsche Wurzelkriterium für das Zweischrittverfahren.

Letzte Änderung am 18.11.04 durch Heinrich Mellmann @Mail: mellmann@mathematik.hu-berlin.de