Es existieren verschieden Verfahren zur Interpolation
einer Population diskreter Punkte. Wir stellen die Polynom- und die
Splineinterpolation gegenüber.
Seien Stützstellen
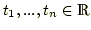 und
Funktionswerte und
Funktionswerte 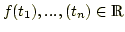 einer Funktion einer Funktion 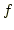 gegeben.
gegeben.
Als Erstes betrachten wir die Interpolation mit Polynomen:
Hierbei wird ein Polynom 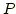 mit
mit 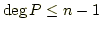 konstruiert das die Interpolationsbedingungen
konstruiert das die Interpolationsbedingungen
erfüllt. Wir bilden
dann gilt
und es ist
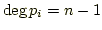 . .
Das Polynom
erfüllt dann alle gestellten Bedingungen.
Dieses Polynom wird das Interpolationspolynom von Lagrange
genannt.
Für praktische Berechnungen wird die Darstellung in Form des Newtonschen Interpolationspolynoms
benutzt.
Als Zweites die Interpolation mit
Natürlichen Kubischen Splinefunktionen:
Bei der Interpolation mittels kubischer
Splinefunktionen wird der Funktionsverlauf innerhalb der einzelnen
Intervalle durch Polynome 3-ten Grades interpoliert. Eine interpolierende
natürliche Splinefunktion kann also geschrieben werden als
wobei die 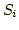 Polynome 3-ten Grades sind. Für die
Polynome
Polynome 3-ten Grades sind. Für die
Polynome 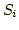 verwendet man den Ansatz verwendet man den Ansatz
wobei 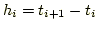 , und , und 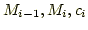 und und 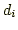 unbekannte Konstanten sind. Zusätzlich werden an die
Splinefunktion
unbekannte Konstanten sind. Zusätzlich werden an die
Splinefunktion 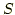 folgende Bedingungen gestellt: folgende Bedingungen gestellt:
- Interpolationsbedingung:
- Stetigkeit der Tangente:
- Stetigkeit der Krümmung:
- ''Natürliche'' Randbedingung:
Mit diesen Bedingungen erhält man ein lineares Gleichungssystem
zur
Bestimmung der Unbekannten Mi.
Bei zunehmender Anzahl der Stützstellen steigt auch der Grad des
Lagrange-/Newton-Polynoms, was dazu führt, dass es im Vergleich
zur
Spline-Funkion besonders stark oszilliert.
Vergleichen Sie das Interpolationsverhalten beider Verfahren bei
verschiedener Anzahl von Stützstellen und deren Verteilung jeweils
für die Runge- und Sinus-Funktion.
|