Quadratische Polynome

  mjwinq.exe  (397 kb).    Quelltext: mj.pas (Turbo Pascal), mjw.pas (Delphi/Lazarus), MandelJulia_X11.c (C/X11).

Untersucht man das Verhalten komplexer quadratischer Polynome unter Iteration, so kann man zuvor jedes Polynom in die Form p(z)=z²+c bringen, d.h. jedes Polynom wird durch einen Parameter c charakterisiert. Die Juliamenge von p_c ist der Rand des Anziehungsbereiches von unendlich.
Die Mandelbrotmenge ist der Parameterraum für die Juliamengen. Dabei gehört ein Parameter c zur Mandelbrotmenge genau dann, wenn die Juliamenge von z²+c zusammenhängend ist. Die Mandelbrotmenge ist zusammenhängend.    (iteration.pdf) (quadpol.dvi)

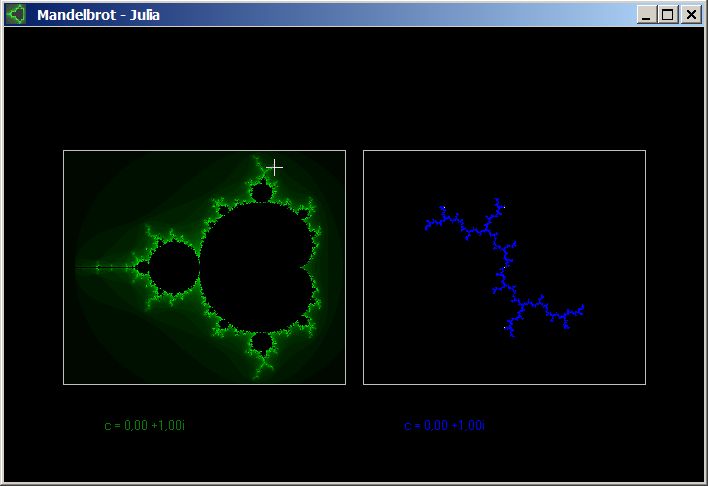
Das Programm zeigt links die Mandelbrotmenge (innerhalb des Grünen), in der man mit der Maus einen Parameter c auswählen kann, zu dem dann rechts die Juliamenge gezeigt wird. Das Programm bietet dazu zwei Möglichkeiten.
Mit der linken Maustaste (blau) wählt man die Inverse Iteration Method, bei der ein Anfangspunkt gewählt wird, der bereits zur Juliamenge gehört. Für diesen Punkt wird der Rückwärtsorbit betrachtet. Jeder Punkt hat zwei Urbilder, wobei sich das Programm für einen entscheidet. Zusätzlich sieht man den Weg, den der kritische Punkt z=0 unter Iteration nimmt. Die Juliamenge ist zusammenhängend genau dann, wenn der Orbit dieses kritischen Punktes beschränkt bleibt.
Wählt man die rechte Maustaste (rot), so wird zu diesem c jeder Punkt z (vorwärts) iteriert und geguckt, ob der Orbit gegen unendlich strebt. Der Rand dieses Anziehungsbereichs von unendlich ist ebenfalls die Juliamenge zu z²+c.

Die Computerbilder sind immer Näherungen der tatsächlichen Juliamengen. Der blaue Algorithmus ist weitaus schneller als der rote, so dass man auch mit gedrückter linker Maustaste durch die Mandelbrotmenge fahren kann. Allerdings zeigt er bei einigen Juliamengen in bestimmten Bereichen nur wenige Punkte. Drückt man die mittlere Maustaste, so werden sogenannte external rays (gelb) gezeichnet, die man sich als Feldlinien vorstellen kann, wenn die (gefüllte) Juliamenge elektrisch geladen wäre. Die Feldstärke ist dort groß, wo auch der blaue Algorithmus eine hohe Dichte zeigt.

Literatur

Computer-Grafik:
H.-O. Peitgen, P. Richter: The Beauty of Fractals, Springer (1986).
H.-O. Peitgen, D. Saupe, H. Jürgens: Chaos: Bausteine der Ordnung, Springer (1994).
H.-O. Peitgen, D. Saupe (eds.): The Science of Fractal Images, Springer (1988).