bzw. in Koordinatenform 
|
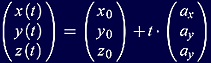
Animationen (durch Trickfilmtechniken oder mithilfe des Computers erzeugte Filme) sind Sequenzen vieler einzelner Bilder (Frames), die sich von Bild zu Bild nur geringfügig ändern. Während einer Animation können sich prinzipiell alle Inhalte und Bildeigenschaften verändern:
Um Computeranimationen zu erzeugen, müssen Bestimmungsgrößen (Koordinaten, Transformationen oder auch z.B. Farbwerte) zeitabhängig beschrieben werden. |
Fasst man in Parameterdarstellungen von Geraden
bzw. in Koordinatenform
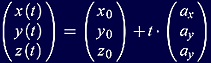
den Parameter t als Zeit auf, so lassen sich Animationen erstellen, bei denen sich
geometrische Objekte auf geradlinigen Bahnen bewegen. In POV-Ray setzt man dazu
clock anstelle von t ein. Durch
sphere { <x0, y0, z0> + clock * < ax, ay, az> r }
lässt sich somit die Bewegung einer Kugel mit dem Radius r auf einer geradlinigen Bahn animieren.
|
||||||
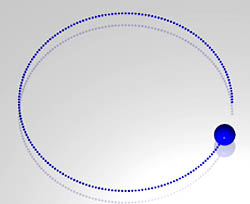
Bei Animationen erhalten Parameterdarstellungen einen Aspekt, der die geometrische Gestalt der durch sie beschriebenen Objekte nicht beeinflusst, nämlich die Geschwindigkeit von Bewegungen. So beschreiben z.B. die beiden Parameterdarstellungen
dieselbe Halbgerade. Werden damit Animationen erzeugt, so ergibt a) eine gleichförmige und b) eine gleichmäßig beschleunigte Bewegung. In der obigen Abbildung ist dies durch die Abstände der Punkte erkennbar; zwischen zwei benachbarten Punkten verstreicht jeweils gleich viel Zeit.
|
Der schräge Wurf ist eine aus einer gleichförmigen (Wurf-) und einer gleichmäßig
beschleunigten (Fall-) Bewegung zusammengesetzte Bewegung. Als Summe einer in t
linearen Komponente und des mit t2 multiplizierten Beschleunigungsvektors
ergibt sich die Gleichung des schrägen Wurfes (welche die Wurfparabel beschreibt):
|
 Video ansehen |
|
Um Objekte auf Kreisbahnen zu bewegen oder einen "Kamerarundflug" über einer Szene zu erzeugen,
müssen Kreise durch Parameterdarstellungen beschrieben werden. Dazu erinnern wir uns daran, wie die Sinus- und die Kosinusfunktion am Einheitskreis eingeführt werden (siehe die Abbildung
rechts):
 durch einen Zeitparameter t (in POV-Ray clock) auszudrücken.
Sollen mehrere Werte animiert werden, ist es günstig, diesen Parameter von 0 bis 1 laufen zu lassen. Dies
erreicht man durch  .
|
|
|
Damit und durch Hinzunahme einer dritten Koordinate (die konstant gehalten wird) erhält man die folgende
Parameterdarstellung für einen
Kreis in der x-z-Ebene des Raumes:
|
 Video ansehen |
|
Oft sollen Animationen erstellt werden, bei denen sich Kameras auf Kurven bewegen und damit die Sicht auf Szenen verändert wird. Wir beginnen mit einer Kamerafahrt auf einer kreisförmigen Bahn. Unter Benutzung der oben angegebenen Parameterdarstellung des Kreises (mit dem Radius 20 und einer "Höhe" y(t)=10 über der x-z-Ebene) lässt sich in POV-Ray eine Kameraanimation auf der entsprechenden Kreisbahn erzeugen:
|
 Video ("Kamerafahrt") ansehen |
|
Verringert man in der Parameterdarstellung eines Kreises während einer Animation allmählich den Radius von einem Anfangsradius r auf 0 (durch Multiplikation des Radius mit 1-t), so erhält man eine archimedische Spirale. In der x-z-Ebene lässt sich diese durch folgende Parameterdarstellung beschreiben:
|
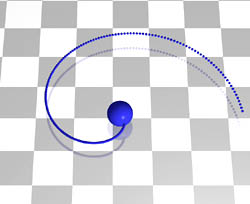 Video: Bewegung einer Kugel auf einer Archimedischen Spirale |
Durch eine Kameraanimation auf einer archimedischen Spirale lässt sich erreichen, dass die Kamera um eine Szene kreist und sich dieser gleichzeitig annähert. Spiralen eignen sich auch gut für Animationen der Zielpunkte von Scheinwerfern, die sich dadurch kreisend von außen dem "Bühnenzentrum" nähern können.
"Kamerafahrt" auf einer Arch. Spirale Video ansehen POV-Ray-Dateien herunterladen |
Animation der Zielpunkte dreier Scheinwerfer auf Spiralen  Video ansehen POV-Ray-Dateien herunterladen |
|
Ersetzt man in der Parameterdarstellung des Kreises die konstant gehaltene Koordinate
y durch eine lineare Funktion
Da |
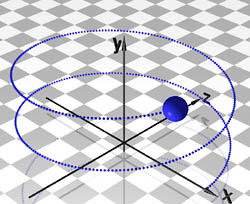 Video: Bewegung einer Kugel auf einer Schraubenlinie |
|
Kombiniert man die Änderungen an der Parameterdarstellung des Kreises, die zur Archimedischen Spirale und zur Schraubenlinie geführt haben, so erhält man eine spiralförmige Kurve, die sich auf einem Kegel entlang windet: eine konische Spirale mit der Parameterdarstellung:
Während der Parameter t (bzw. die Zeit clock) von 0 bis 1 wächst, verringert sich der Abstand der Punkte der Kurve von der y-Achse von r auf 0. Gleichzeitig steigt die Höhe y von 0 auf h. Konische Spiralen eignen sich besonders gut als Bewegungsbahnen für Kameraanimationen, da die Kamera um eine Szene "kreist" und sich dabei gleichzeitig sowohl die Höhe, aus der die Szene betrachtet wird, als auch der Abstand von der Szene verändert.
Gegenüber der oben angegebenen Parameterdarstellung wurde für die hier zu betrachtende Kameraanimation
|
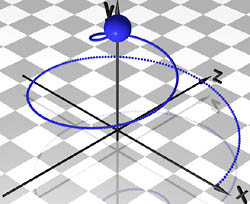 Video: Bewegung einer Kugel auf einer konischen Spirale  Video: "Kamerafahrt" auf einer konischen Spirale |
Die Verwendung eines Zeitparameters in Parameterdarstellungen ist nicht die einzige Möglichkeit, Animationen zu generieren. Auch geometrische Transformationen (z.B. Verschiebungen, Drehungen und Streckungen) können animiert, also zeitabhängig verändert werden. Wichtig ist dabei oft die Reihenfolge, in der Transformationen ausgeführt werden und die richtige Synchronisation verschiedener Bewegungen.
Möchte man die Drehung der Erde um sich selbst, des Mondes um die Erde sowie des Mondes um sich selbst simulieren, so ist darauf zu achten, dass (bei im Koordinatenursprung befindlichem Mondmittelpunkt) zunächst eine Drehung (Drehung des Mondes um seine eigene Achse), danach eine Translation (Verschiebung) und schließlich erneut eine Drehung (Mondbewegung um die Erde) ausgeführt werden müssen.
|
In POV-Ray lässt sich die Erd- und Mondbewegung folgendermaßen nachbilden: Der Abstand des Mondes von der Erde wurde nicht maßstabsgetreu berücksichtigt, da Erde und Mond dann kaum zu erkennen wären. |
 Video: Erde und Mond |
Um eine Kugel auf einer Ebene entlang rollen zu lassen, sind eine Drehung und eine Translation zu kombinieren. Dabei müssen die Winkelgeschwindigkeit der Drehung und die Translationsgeschwindigkeit so synchronisiert werden, dass der in einer Zeiteinheit durch die Verschiebung zurückgelegte Weg gleich der Bogenlänge des durch den Drehwinkel beschriebenen Kreisbogens ist, auf dem die Kugel rollt.
|
In dem unten angegebenen Beispiel bewegt sich die Kugel durch Translation in einer Zeiteinheit um 6
Längeneinheiten und dreht sich um den Winkel Die unterschiedlichen Vorzeichen sind notwendig, da sich Punkte der Kugeloberfläche, wenn sie beim Rollen den "Boden" berühren, aus Sicht der Kugel entgegengesetzt zur Rollrichtung bewegen.
|
 Video: Rollende Kugel |
Andreas Filler, 2007
- Ortsvektor des Abwurfpunktes
- Vektor der
Anfangsgeschwindigkeit
- Erdbeschleunigungsvektor
des Parameters 
(statt in der 
) bei 
eingesetzt
wurde, hat die Schraubenlinie 2 "Windungen" (der "überstrichene" Winkel beträgt
, also 720°).
statt 
.
,