Viele Flächen lassen sich durch Funktionsgleichungen beschreiben, indem die Höhenkoordinaten (z.B. y oder z) von Punkten als Funktionen der beiden anderen Koordinaten ausgedrückt werden:
z = f(x,y) ![]() oder
oder
![]() y
= f(x,z).
y
= f(x,z).
Welche der Koordinaten die Höhenkoordinate ist, hängt davon ab, welches dreidimensionale Koordinatensystem verwendet wird. Die folgenden Beispiele sind unter Verwendung eines Koordinatensystems angegeben, in dem standardmäßig die y-Achse senkrecht dargestellt wird. (Ein solches Koordinatensystem nutzt auch die auf diesen Seiten oft erwähnte Software POV-Ray.)
|
|
SattelflächenDie wie "UFOs", "fliegende Teppiche" oder "Schmetterlinge" aussehenden Objekte rechts oben in dem Bild auf der Startseite bestehen aus Kugeln und sogenannten Sattelflächen, die in dem Ray-Tracing-Programm POV-Ray mit unterschiedlichen Farbmustern versehen wurden. Sattelflächen lassen sich durch recht einfache quadratische und kubische Funktionen beschreiben, wobei zwei unabhängige Variable (z.B. x und z) notwendig sind und die dritte Koordinate (die "Höhe", z.B. y) als Funktion dieser Variablen ausgedrückt wird. Der hier in einer schematischen Darstellung gezeigte "Affensattel" wird durch die Funktionsgleichung y = f(x,z) = x3 - 3 x z2 beschrieben. Betrachtet man die einzelnen Kurven in der schematischen Darstellung, so kann man in der einen Richtung kubische Parabeln und in der anderen Richtung "normale" quadratische Parabeln erkennen. Das ist kein Wunder, denn es handelt sich um Koordinatenlinien - Kurven, für die eine der Variablen x oder z konstant ist. Setzt man in der Gleichung für x oder für z eine feste Zahl ein, so erhält man ganz normale Graphen von quadratischen (falls x konstant gehalten wird) oder kubischen Funktionen (wenn z konstant bleibt). |
Durch Funktionsgleichungen lassen sich bereits viele Flächen darstellen, interessante Formen erhält man z.B. durch die Verwendung von Sinus- und Kosinusfunktionen.
|
Klicken Sie auf die Vorschaubildchen, um größere Abbildungen zu betrachten und die entsprechenden POV-Ray-Beispieldateien herunterzuladen. |
||||
Beschreibungen von Flächen durch Funktionsgleichungen versagen, wenn Flächen beschrieben werden sollen, bei denen mehrere Punkte unterschiedlicher "Höhe" über einem Punkt der x-y-Ebene bzw. der x-z-Ebene liegen (wie z.B. bei Kugeln). Eine Verallgemeinerung für diesen Fall stellt die Beschreibung von Flächen durch implizite Gleichungen dar:
f(x,y,z) = 0 .
Einige Beispiele durch implizite Gleichungen beschriebener Flächen:
|
Klicken Sie auf die Vorschaubildchen, um größere Abbildungen zu betrachten und die entsprechenden POV-Ray-Beispieldateien herunterzuladen. |
||||
In POV-Ray lassen sich durch implizite Gleichungen gegebene Flächen durch die "isosurface"-Anweisung beschreiben, siehe die Kurzanleitung Parametric+Isosurface.
Die unten abgebildete Fläche wird durch eine Gleichung 6. Ordnung beschrieben. Laden Sie die Datei herz.pov herunter und experimentieren Sie damit.
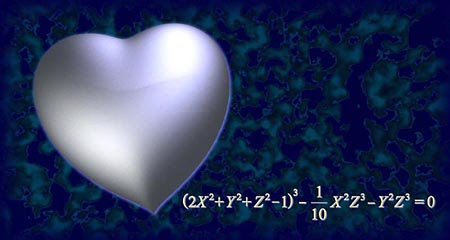
Für kompliziertere Flächen müssen alle drei Raumkoordinaten in Abhängigkeit von zwei Parametern u und v angegeben werden:
x = f1(u,v) ; ![]() y = f2(u,v) ;
y = f2(u,v) ;
![]() z = f3(u,v) .
z = f3(u,v) .
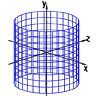
Ein Beispiel ist die Parameterdarstellung einer Kugeloberfläche (mit dem Radius r):
|
x(u,v) = r cos u cos v y(u,v) = r sin v z(u,v) = r sin u cos v |
0 < u < 2 |
Lässt man einen der Parameter u und v fest, so beschreibt die Parameterdarstellung eine Kurve (siehe Parameterdarstellungen von Kurven), genannt Parameterlinie. Die Parameterlinien einer Kugel sind Meridiane (mit u = const.) und Breitenkreise (mit v = const.). Beginnt man mit kleinen Intervallgrenzen für die Parameter und vergrößert diese allmählich, so kann man den Aufbau einer Fläche entlang der Parameterlinien in einem Video darstellen (siehe unten rechts).
|
|
|
In POV-Ray lassen sich durch Parameterdarstellungen gegebene Flächen mithilfe der Anweisung "parametric" darstellen, siehe dazu die "Kurzanleitung Parametric+Isosurface". Die folgenden Beispiele können Ihnen vielleicht Anregungen für eigene Experimente geben.
|
|

|

|
|

|
| Klicken Sie auf die Vorschaubildchen, um größere Abbildungen zu betrachten und die entsprechenden POV-Ray-Beispieldateien herunterzuladen. | |||||
|
Ein wunderschönes Beispiel einer Fläche, die durch eine Parameterdarstellung beschrieben werden kann, ist die Dini-Fläche, benannt nach dem italienischen Mathematiker Ulisse Dini, 1845-1918. Die Parameterdarstellung der Dini-Fläche ist
In der nebenstehenden Abbildung laufen die Parameter u bis 4 Die POV-Ray-Datei, mit der die Abbildung der Dini-Fläche erzeugt wurde, können Sie herunterladen und variieren. |

|
|
|
Die Kleinsche Flasche (benannt nach dem Mathematiker Felix Klein, 1849 - 1925) gehört sicherlich zu den interessantesten Flächen. Es handelt sich um eine "nicht orientierbare" Fläche, das heißt "Innen" und "Außen" können nicht voneinander unterschieden werden. Läuft man auf einer der Linien die Flasche entlang, so gelangt man ohne Übergang von Innen nach Außen und umgekehrt - gut ist dies in der Drahtgitterdarstellung zu erkennen. Sie können auch eine interaktive (dreh- und skalierbare) Darstellung der Kleinschen Flasche betrachten. Die Beschreibung der Kleinschen Flasche durch Gleichungen ist nicht ganz einfach. Man benötigt dazu Parametergleichungen, in denen für zwei Bereiche des Parameters u verschiedene Gleichungen auftreten. Parametergleichungen der Kleinschen Flasche:
Für
Für 0 < u <
|
Andreas Filler, 1996-2007
