Grundkurs Gnuplot
Sommersemester 2002, Freie Universität Berlin
Autor: Dr. David Völker
Institut für Geowissenschaften, Freie Universität Berlin, Malteserstr.74-100, D-12249 Berlin; Raum B138, tel: 70-289
email: voelker@zedat.fu-berlin.de

Grundkurs GnuplotSommersemester 2002, Freie Universität Berlin |
 |
Inhalt:
|
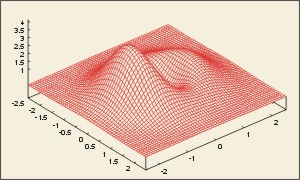
Beispiel für die Darstellung einer 3-D-Funktion mit Gnuplot |
Gnuplot ist ein kommandozeilen-orientiertes, interaktives wissenschaftliches Plotprogramm. Es ist klein, mächtig und macht all das, was man braucht, um Daten schnell darzustellen: Gnuplot kann sowohl Kurven (x/y-Datenpaare) als auch 3D-Objekte (Flächen) abbilden. (An dieser Stelle ein grosses Danke für ein grosses Programm!).
Gnuplot ist umsonst und wird als Programmcode verteilt** (siehe links zu Gnuplot). Das hat unmittelbare Vorteile, natürlich wegen der Kosten, die man für andere software aufbringen müsste, aber auch deshalb, weil man die Programme für jede Sorte von Rechnerarchitektur passend kompilieren kann. - allerdings auch muss, denn es wird keine fertige Software geliefert. - allerdings gibt es mit wgnuplot bereits eine fertig für Windows aufbereitete Version mit aufgesetzter Benutzeroberfläche.
** es handelt sich um freeware in dem Sinne, dass es "for free" also umsont zu beziehen ist, aber nicht in dem Sinne, dass es erlaubt wäre den Programmcode zu verändern, sowie eigene Versionen zu vertreiben.
Mit Gnuplot lassen sich Funktionen und Daten (Messwerte) in einem zweidimensionalen karthesischen Koordinatensystem oder in einem 3D-Raum darstellen. Flächen werden dabei als Netzgittermodell im 3dimensionalen Raum dargestellt oder als Kontur in die x-y-Ebene projeziert. Für 2D-Darstellungen stehen zahlreiche Arten der Darstellung (Styles) zur Verfügung, wie z.B. Linien, Punkte, Linien mit Punkten, Balken. Die Kurven und Achsen können mit Werten versehen werden, Markierung, Überschriften, Datums-und Zeitangaben etc. sind möglich. Die Hauptanwendung besteht vor allem darin, Wertepaare, die man aus Berechnungen, Messungen etc. erhalten hat darzustellen. Zusätzlich zu dieser Aufgabe können beliebige Funktionen (Polynome, trigonometrische Funktionen ...) geplottet werden und Interpolationen durchgeführt werden, d.h. Polynome als "best fit" durch gemessene Wertepaare gelegt werden. Zusätzlich zum üblichen karthesischen Koordinatensystem kennt Gnuplot auch polare Koordinatensysteme.
3D-Interpolation (gridding) zwischen unregelmäßig verteilten Datenpunkten (ein häufiges Problem) ist mit einem einfachen Gewichtungsverfahren möglich, andere Programme (z.B. Surfer) bieten in dieser Hinsicht weit mehr Möglichkeiten, aber für viele Ansprüche dürfte es bereits genügen.
Tortendiagramme sind nicht die Stärke von Gnuplot. Ebenso -soweit mir bekannt- ternäre Diagramme, was für Geologen natürlich schade ist ...
Gnuplot ist wie gesagt ein kommandozeilen-orientiertes, interaktives Programm, d.h. beim Aufruf erscheint ein Kommandofenster mit folgendem Prompt: (gnuplot>), das eine Eingabe
verlangt, z.B. einen der Plotbefehle oder die Definion einer Funktion
oder Angaben zur Formatierung einer Achse oder etwas ähnliches. Ist
eine Eingabe erfolgt, wird sie ausgeführt, was man entweder sofort
merkt (bei einem Plotbefehl) oder sich später auf folgende Plotbefehle
auswirkt (bei Funktionsdefinitionen z.B.)
gnuplot> a=0.25 gnuplot> f(x)=sin(x)*a gnuplot> plot f(x)
Diese Befehlsabfolge (jeweils mit einem ENTER abgeschlossen) hätte z.B. das folgende Resultat:
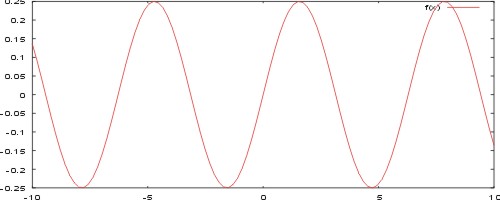
Praktischerweise wird man diese Befehlsfolgen nicht immer wieder neue eingeben, sondern in eine Stapeldatei oder Script-Datei (eine einfache Textdatei, in Folgenden einfach plt-Datei genannt) schreiben, die dann aufgerufen werden kann (Befehl: load 'Datei.plt')
und die Befehlsabfolge in Gang setzt. So kann man eine Datei immer
weiter editieren, z.B. um die Achsenlänge zu verändern, dasselbe
Grafikformat auf unterschiedliche Daten loszulassen etc.
Es gelten schon einige vordefinierte Standard-Einstellungen über den
Stil der Abbildung z.B. daß die erste Grafik in rot gehalten wird etc.
Angezeigt werden die gültigen Einstellungen mit dem Befehl show all. Diese Grundeinstellungen stehen in einer Datei namen .gnuplot (UNIX, LINUX), bzw. GNUPLOT.INI(Windows).
Diese defaults kann man natürlich überschreiben. Der prinzipielle
Befehl, um Änderungen an Achsen, Label, Wertebereiche etc. vorzunehmen
lautet set. Eine Änderung wirkt sich solange aus, bis man die Einstellungen neu festgelegt hat. Mit reset kehrt man zu den Standardeinstellungen zuück.
Im Folgenden werden einzelne wichtige Befehle und Funktionen
vorgestellt und illustriert, was sie bewirken. Zu jedem der Befehle
existiert eine detaillierte Beschreibung, die mit dem Befehl help abfragen kann (z.B. help set).
Die Beispiels-skriptdateien bauen teilweise aufeinander auf, es kommt
immer etwas neues dazu. Sie können am Ende der Seite auch
heruntergeladen werden, um sie z.B. als Vorlage für eigene Grafiken zu
verwenden.
Die symbolisierten Papierkanten sollen Anfang und Ende der Datei darstellen (sieht zwar eher wie eine Tapete aus...).
|
# Einfacher Polynom 03/02 #========================================== set xrange [-5:10] set yrange [-150:250] a=0.7 b=-2.0 c=-25 f(x)=a*x**3+b*x**2+c*x-12 plot f(x)
|
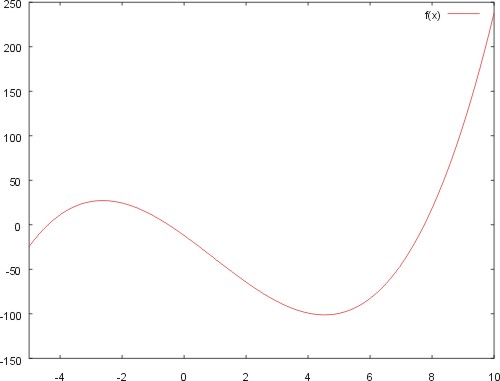 |
Was passiert hier? Zunächst einmal werden die darzustellenden
Achsenbereiche festgelegt: x von -5 bis 10, y von -150 bis 250, dann
werden einige Variablen definiert, die dann später in der
Funktionsdefinition wieder aufgegriffen werden. Der Plot-Befehl plot f(x) stellt die Funktion dar.
|
# Plotten von gemessenen Daten 03/02 #==================================== set title 'NaCl-Konzentrationen entlang Profil 17b' set yrange [0:600] set xrange [2:17] set xlabel 'Entfernung [km]' set ylabel 'Konzentration [ppm]' plot 'Nacl_17b.dat' using 1:2 with points
|
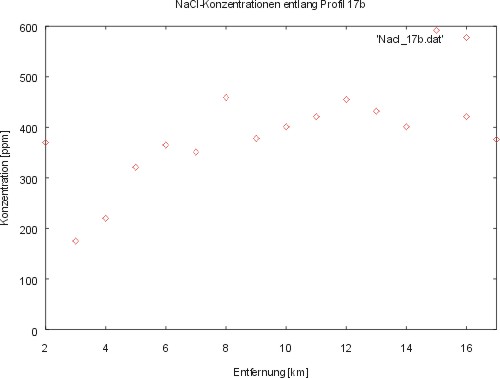 |
Was ist dazugekommen? mit set title wurde die Grafik beschriftet, mit set xlabel und set ylabel
die Achsen beschriftet. Im Unterschied zum vorigen Beispiel wird hier
keine Funktion dargestellt, sondern gemessene Daten, die aus einer
Datei (Nacl_17b.dat) bezogen werden. Es handelt
sich um eine einfache Textdatei, in der die x/y-Wertepaare
(Konzentration gegen Entfernung) als zwei Spalten (getrennt je durch
ein paar Leerzeichen) stehen. So etwas könnte z.B. eine aus EXCEL
exportierte Datei sein. Man kann einzelne Spalten einer Datei
gegeneinander darstellen (z.B. 3. Spalte =x, 1. Spalte = y) durch den
Zusatz
using 3:1Diese Anwendung beeinhaltet noch weitere Möglichkeiten:
plot 'datenfile.dat' using 1:($4>5 ? $4 :1/0)- Datenclipping: plotte Spalte 1 (x) gegen Spalte 4 (y), wenn y>5
plot 'datenfile.dat' using 1:($4*(-1))- Berechnen der Spalten: plotte Spalte 1 (x) gegen Spalte 4(y), multipliziert mit -1
Die Daten sollen nicht verbunden werden, sondern als Punkte dargestellt werden, daher das Zauberwort with der den plot-Befehl mit einem STYLE verbindet (für genauere Angaben betätigen Sie help plot).
|
# Plotten von berechneten Daten 03/02 #==================================== set title 'Kriechfestigkeit der Kruste' set yrange [-30000:0] set xrange [1e5:1e11] set logscale x set pointsize 0.5 set grid set xlabel 'Differenzspannung [Pa]' set ylabel 'Teufe [m]' plot 'creep_qz.dat' title "Quarz" with points, \ 'creep_halit.dat' title "Halit" with points, \ 'creep_granit.dat' title "Granit" with points
|
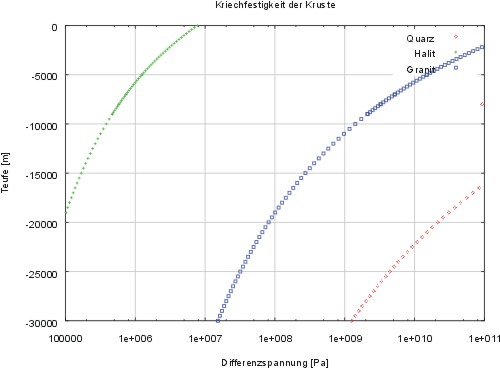 |
Was ist dazugekommen? mit set title wurde die Grafik beschriftet, mit set grid ein Gitternetz gelegt und mit set logscale x
die x-Achse logarithmisch unterteilt, um den großen Werteberich der
Daten darstellen zu können. Wie im vorherigen Beispiel werden die Daten
aus Dateien bezogen (creep_qz.dat, creep_halit.dat und creep_granit.dat),
um sie übereinander in denselben Grafen zu plotten werden sie mit einem
Komma aneinander gehängt. Die Dateien sind wiederum schlichte
Textdateien mit 2 Spalten für x und y -Werte.
|
# least squares fit an gemessenen Daten 03/02 #============================================ set title 'NaCl-Konzentrationen entlang Profil 17b' set yrange [0:600] set xrange [2:17] set xlabel 'Entfernung [km]' set ylabel 'Konzentration [ppm]' f(x)=a*x**3+b*x**2+c*x+d fit f(x) 'Nacl_17b.dat' via a, b, c, d plot 'Nacl_17b.dat' with points, f(x)
|
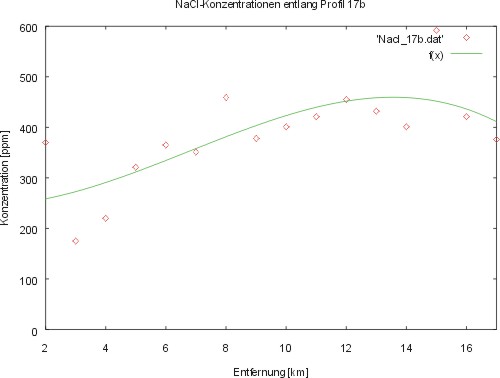 |
Diesmal etwas ganz anderes: Häufig wollen wir eine Funktion durch
eine Wolke von Messergebnissen legen, da der Verdacht besteht, daß die
Messgrößen in irgendeiner Form voneinander abhängig sind. Mit Gnuplot
können wir den Polynom finden, der am besten durch die Punktwolke
passt. Das Verfahren nennt sich "least squares fit" und besteht -kurz
gesagt- darin, die Kurve zu finden, bei der die Summe der Abweichungen
(zum Quadrat) zwischen Kurve und einzelnen Messpunkten minimal ist. Wir
geben eine Funktion vor, z.B. f(x)=a*x**3+b*x**2+c*x+d (Polynom 3.
Grades) und wollen die Werte von a, b, c und d erhalten für die das
eben genannte Kriterium gilt. Der Befehl heißt fit.
Anschließend können wir noch Datenpunkte und Kurve übereinander
plotten. Ob der fit in diesem Fall sehr sinnvoll ist, sei hier mal
irrelevant, es geht um das wie.
|
3D-Darstellung 03/02 #========================================== set xrange [-49.28:-49.13] set yrange [12.05:12.20] set zrange [-5000:-3750] set view 45,20,1.0,2.5 splot 'topo.xyz'
|
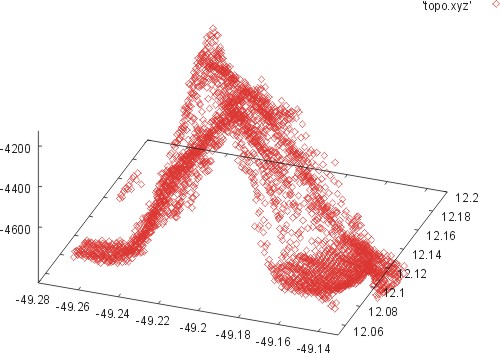 |
Der Schritt in die 3.Dimension ist nicht schwer: zusätzlich muss ein Wertebereich der z-Achse festgelegt werden (set zrange), sowie ein Blickwinkel und -höhe (Azimuth & Elevation mit set view). Statt plot heißt der Befehl nun splot. Die Datenpunkte werden einer Datei entnommen (topo.xyz) bei der es sich wiederum schlichte Textdatei mit 3 Spalten für x- y- und z-Werte handelt.
|
set hidden3d set isosamples 40 set xrange [-2.5:2.5] set yrange [-2.5:2.5] set zrange [0.0:5.0] set xtics 0.5 set ytics 1.0 set ztics 0.5 set view 40,50,1.0,1.5 f(x,y)=(x**2+2.5*y**2-y)*exp(1-(x**2+y**2)) splot f(x,y)
|
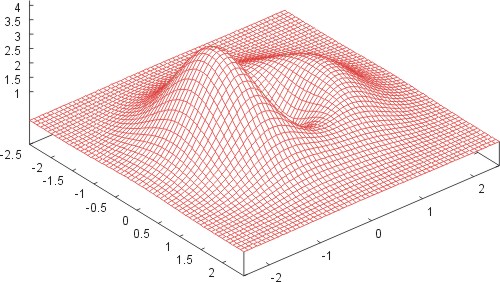 |
Anstelle von Meßwerten können auf 3dimensionale Funktionen f(x;y)
als Flächen im Raum dargestellt werden. Dazu müssen die Achsenbereiche
von x-, y- und z-Achse festgelegt werden (z.B. set zrange), sowie ein Blickwinkel und -höhe (Azimuth & Elevation mit set view, hier 40° und 50°). Nachdem die Funktion definiert wurde, kann sie direkt dem Befehl splot
übergeben werden. Da hier keine diskreten Werte vorliegen, braucht es
noch eine Angabe darüber, wie dicht die Gitternetzlinien gesetzt werden
sollen (set isosamples). Um den 3D-Effekt zu erhalten, können verdeckte Liniensegmente (die, welche man nicht sehen würde) ausgeblendet werden (set hidden3D)
|
set data style lines set contour base set surface set xrange [-5:400] set yrange [0:510] set zrange [-20:70] set view 50,10,1.0,1.0 set dgrid3d 40,51,3 show contour splot 'surface.xyz'
|
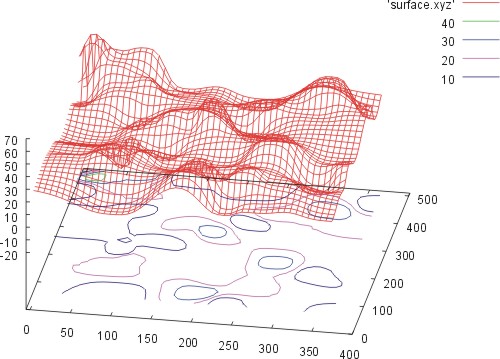 |
Ein Datensatz (einfache 3-spaltige Tabelle) mit unregelmäßig verteilten Datenpunkten (scattered data, hier die Datei surface.xyz)
soll als Netzgitter-Oberfläche und als Konturlinie (projeziert auf die
Grundfäche) dargestellt werden. Dafür müssen zunächst durch
Interpolation die Lücken gefüllt und ein equidistantes Netz von
Datenpunkten geschaffen werden (gridding). Das Verfahren besteht darin,
daß jeder Datenpunkt in Bezug auf einen Gitterpunkt zu dessen Wert
beiträgt und zwar gewichtet nach seiner Entfernung zu diesem und einem
Gewichtungsfaktor. Das Gridden des Datensatz erfolgt mit dem Befehl dgrid3d.
Der Befehl braucht als Angabe die Anzahl von Intervallen in x-Richtung
und y-Richtung (hier: 40 und 51), die den Grid ausmachen und einen
Gewichtungsfaktor (dazu unten mehr).
Beim Gridden sollte man sich dessen bewußt sein, was man tut: aus
ein paar vorhandenen Datenpunkten wird eine ganze Welt errechnet! Man
interpoliert Lücken, indem man annimmt, daß die Punkte in der Nähe von
Messwerten sich so ähnlich wie diese verhalten. Der Grid kann natürlich
nur so gut sein, wie die Datendichte und Datenqualität es zulässt. Auch
wenn man aus wenigen Datenpunkten optisch viel zaubern kann, ist es oft
korrekter die Lücken zu bekennen. Durch das Gewichtungsverfahren, die
Dichte des Grids und die Gewichtungsfaktoren kann man beeinflussen, wie
groß der Einfluss eines Messwertes auf seine Umgebung ist: Je weiter
der Radius um einen Gitterpunkt ist, innerhalb dessen Messwerte in die
Berechnug des Knotenpunkts merklich eingehen, desto weniger spielen
lokale Maxima eine Rolle und desto optisch glatter wird das Ergebnis.
Ein Beispiel mit demselben Datensatz wie oben und unterschiedlichen
Gewichtungsfaktoren des Befehls dgrid3d wird hier gegeben:
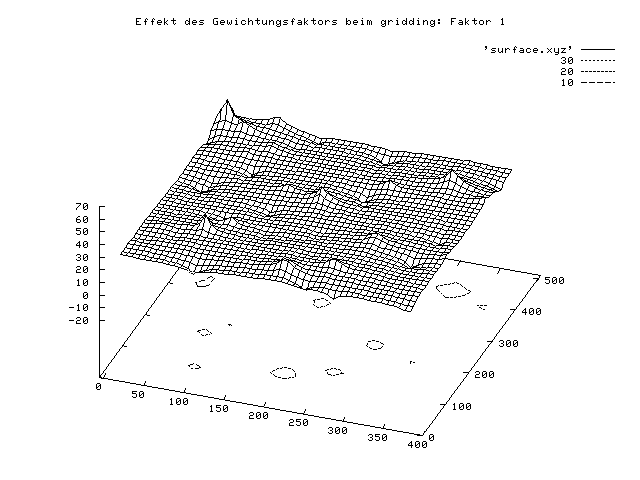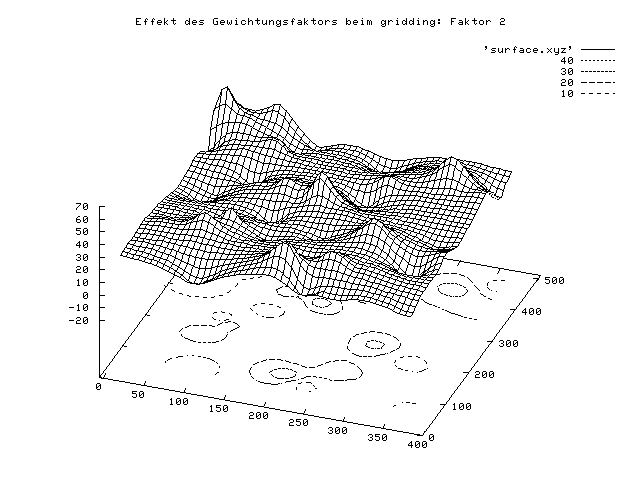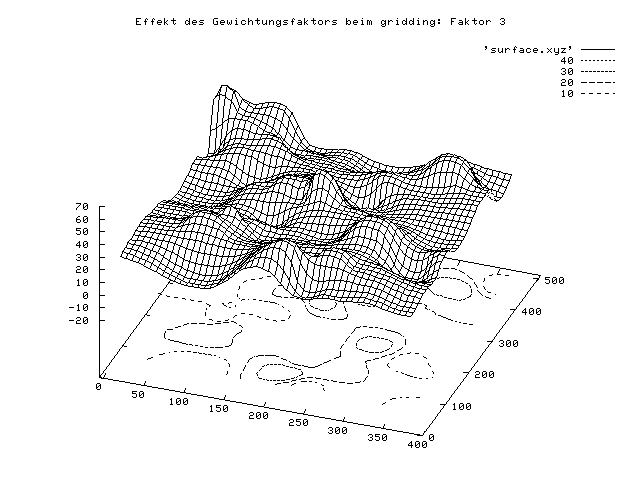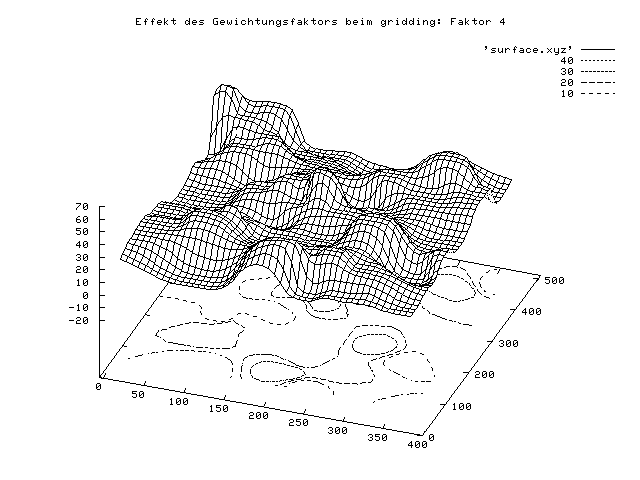
Man kann die Grafik direkt in die Zwischenablage kopieren und in ein Grafikprogramm (z.B. Corel Draw) einfügen, oder die Grafik z.B. in eine Postscript-Datei lenken. Postscript ist eine Vektorgrafik-Beschreibungssprache, die von vielen (eben postscript-fähigen)-Druckern interpretiert werden kann, insofern ohne Druckertreiber direkt von Drucker verstanden wird, wird aber auch von vielen Grafikprogrammen interpretiert. Für den Einbau in Publikationen bietet sich das sogenannte encapsulated Postsript (eps) - Format an. Für das Erzeugen einer Postscript-Datei reicht es aus, an die Befehle die folgenden 3 Zeilen anzuhängen:
| Erzeugen von Postscript-Datei | Erzeugen von Encapsulated Postscript-Datei |
|---|---|
set output "datei.ps" set terminal postscript replot |
set output "datei.eps" set terminal postscript eps replot |
datei steht hier für irgendeinen beliebigen
Dateinamen. Neben Postscript sind auch andere Grafik-Formate möglich,
z.B. PING (png). Näheres erfährt man mit dem Befehl set terminal.
| Gnuplot-Code | Wirkung |
|---|---|
set xtics rotate 1 |
rotate bewirkt eine Drehung der Achsenbeschriftung um 90°, die 1 bewirkt, daß jeder xtic beschriftet wird (2 entsprechend jeder zweite ...) |