
|
Thomas Neukirchner
Humboldt Universität zu Berlin
Reine Mathematik
Rudower Chausse 25
Haus 1, Raum 310
D-12489 Berlin
Phone: +49-30-2093-1826
e-mail:
neukirch@mathematik.hu-berlin.de
Private:
Ebersstr. 37 10827 Berlin Phone: +49-30-78713284 |
|
- Bis August 2009 Assistent von Prof. Helga Baum im Bereich "Differentialgeometrie und Globale Analysis "
- Seit September 2009 Lehrer für Mathematik und Physik an der Freien Waldorfschule Karlsruhe
Gliederung der Seite:
- Lehrveranstaltungen
- Übungsmaterial
- Vortragsfolien
- Eine "Holonomie-Maschine"
- Planimeter
- Goldener Schnitt und Fibonacci-Zahlen bei Pflanzen (Phyllotaxis)
- Researchinterest and Preprints
Lehrveranstaltungen früherer Semester:
- SS07 Übung Analysis III bei Prof.Baum
- WS06 Übung Analysis II bei Prof. Baum
- WS05 Proseminar: Ausgewählte Kapitel der Differentialgeometrie (Kurven- und Flächentheorie)
- SS05 Übung Analysis II bei
Prof. Schüth, Differentialgeometrie
I bei Prof. Baum
- WS04 Übung Topologie
bei Prof. Klaus Mohnke
- SS04 Übung Lineare Algebra und Geometrie II bei Prof. Klaus Mohnke
- WS03 Übung Lineare Algebra und Geometrie I bei Prof. Klaus Mohnke
- SS03 Übung Differentialgeometrie II bei Prof. Baum
- WS02 Übung Differentialgeometrie I bei Prof. Baum
- SS02 Übung Analysis IV bei Prof. Baum
Übungsmaterial & Aufsätze:
Differentialgeometrie:
- Geodäten, Wellenfronten und Konjugierte Punkte auf dem
Torus: [Torus.pdf]
- Differentialoperatoren 1. Ordnung, Bochner-Technik, parallele Vektorfelder: [Diffop.pdf]
- Bilder zur Hopf-Faserung: [Hopf-Faserung.pdf]
- Divergenz, Rotation und Scherung eines Vektorfeldes: [Vektorfeld.pdf]
- Begleitende Repere von Kurven und Dynamik starrer Körper: [Starrerkoerper.pdf]
- Kleine Ausarbeitung zu Planimetern: [Planimeter.pdf]
- Einige illustrative Beispiele zum Kommutator von Vektrofeldern - z.B. Einparken: [Kommutator.pdf]
- Euklidischer Algorithmus und Inverse in Z/pZ (mit Beispielen): [Euklid.pdf]
- Ein Rätsel: Unterhalung zweier Mathematiker...: [Sumprod.pdf]
- Vergleich verschiedener Definitionnen von
Simplizialkomplexen: [Simplizial.pdf]
- Das Banach-Tarski-Paradox: [Banach-Tarski.pdf]
- Simulation der Schwingueiner angezupften Saite (Matlab-Programm): [saite.m]
Vortragsfolien:
- Dualismus: Von der Anschauung zum Formalismus Vortrag im Seminar von Prof. H.-L.
Schön im SS06 [Licht.pdf]
- Können Pflanzen zählen? Vortrag bei der Langen Nacht der Wissenschaften 2006 [Phyllotaxis.pdf]
- Krumme Kurven in geraden Räumen - gerade Kurven in krummen
Räumen Vortrag beim Tag der
Mathematik 2006 [Krumme_Kurven.pdf]
[Gerade_Kurven.pdf]
- Alles Relativ... Differentialgeometrie zwischen Mathematik und Physik Vortrag bei der Langen Nacht der Wissenschaften 2005 [Alles_relativ.pdf]
- Beispiele homogener Lorentzräume mit spezieller Holonomie Vortrag beim Workshop
´Transformationgroups in pseudo-Riemannian geometry´
Leipzig 2006 [Homogen.pdf]
Planimeter:


Unsere Aufmerksamkeit wurde auf die
wundersam einfache Konstruktion der Planimeter gelenkt, da
sie eine schöne Anwendung des Stoke'schen Integralsatzes
darstellt. Noch vor einem Jahrzehnt sicherlich ein unverzichtbares
Hilfsmittel in Geographie und Ingenieurswissenschaften, dürften
diese teils ausgeklügelten Geräte vom Austerben bedroht sein
und alsbald in Vitrinen verstauben. Dennoch haben wir einiges bei der
Beschäftigung mit diesen geometrischen 'Analogrechnern' aus
der prädigitalen Urzeit gelernt:[Planimeter.pdf]
Besonders empfehlenswert ist die Internetseite von [Robert l. Foote]. Der Beweis der isoperimetrischen Ungleichung mithilfe der Planimeter und ihre Holonomietheoretische Behandlung sind dabei bei weitem nicht offensichtlich. Beim Nachbau eines Planimeters sind wir vom gängigen Konstruktionsprinzip eines teils rollenden, teils gleitenden Rades (siehe obige Abbildungen aus F.Murray: Mathematical Machines, Vol.2, Analog Devices) abgewichen und haben eine rollende Kugel dazwischen geschaltet. Dieses mechanische System ist holonom und eignet sich ausserdem zur Veranschaulichung der Parallelverschiebung auf der Sphäre.
Besonders empfehlenswert ist die Internetseite von [Robert l. Foote]. Der Beweis der isoperimetrischen Ungleichung mithilfe der Planimeter und ihre Holonomietheoretische Behandlung sind dabei bei weitem nicht offensichtlich. Beim Nachbau eines Planimeters sind wir vom gängigen Konstruktionsprinzip eines teils rollenden, teils gleitenden Rades (siehe obige Abbildungen aus F.Murray: Mathematical Machines, Vol.2, Analog Devices) abgewichen und haben eine rollende Kugel dazwischen geschaltet. Dieses mechanische System ist holonom und eignet sich ausserdem zur Veranschaulichung der Parallelverschiebung auf der Sphäre.
Eine "Holonomie-Maschine":
Geodäten:
Geodäten verallgemeinern den Begriff der Geraden in der Euklidischen Geometrie auf gekrümmte Räume. Für Flächen gibt es viele Möglichkeiten, die Geodäten physikalisch zu interpretieren und zu realisieren: als kürzeste Verbindungen zweier Punkte lassen sie sich mit Hilfe eines Gummibands darstellen. Als die am wenigsten gekrümmten Kurven werden sie durch einen Stab verkörpert, der zwischen zwei Kopien der Fläche eingeklemmt ist und als die frontalsten Kurven treten sie in Erscheinung als Linien senkrecht zu einer Wellenfront, bzw. als Weg eines 2-rädrigen Wagens, dessen Räder mit einer starren Achse infinitesimaler Breite verbunden sind. All diese Phänomene geben uns Möglichkeiten an die Hand, physikalisch "gerade" Weg in einer Fläche zu finden, wobei es durchaus erstaunlich ist, dass all diese Phänomene auf denselben Begriff der Geodäte führen:
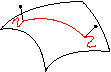
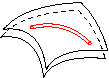
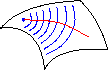
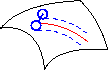
Parallelverschiebung:
Folgen wir nun beliebigen, also nicht notwendig geradlinigen Wegen in der Ebene, können wir uns trotzdem "merken", welches die ursprüngliche Richtung war, in die wir geschaut haben. Wir wollen sozusagen eine Art Kompass mit uns führen, der die Abweichung vom geraden Weg anzeigt. Geometrisch machen wir dabei nichts anderes als die Anfangsrichtung parallel zu verschieben. Auch auf gekrümmten Flächen kann man den Begriff des Parallelverschiebens einführen und wir suchen, wie im Fall der Geodäten, nach einer intuitiv verständlichen, physikalischen Interpretation. Z.B. kann man den oben erwähnten 2-rädrigen Wagen so abändern, dass man mit ihm auch längs Kurven fahren kann, ein auf ihm montierter Zeiger aber stets die parallelverschobene Richtung anzeigt. Eine solche Zahnradkonstruktion war vermutlich schon dem chinesischen Kaiser Huang-Di vor mehr als 5000 Jahren bekannt. Ein schöner Aufsatz hierzu ist von Prof.D.-E.Liebscher: "Mit dem Kompasswagen über den Globus". In dieser technischen Form wird uns die Paralleverschiebung allerdings niemals in der Natur in Erscheinung treten.
Foucault'sches Pendel und ein ähnliches Rad:
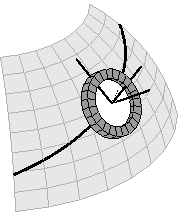 Auf
der Suche nach einer direkten physikalischen Entsprechung für
den Paralleltransport stößt man auf das Foucault'sche
Pendel, mit dem 1851 der Nachweis gelang, dass sich die Erde dreht. Aus
physikalischer Sicht
Auf
der Suche nach einer direkten physikalischen Entsprechung für
den Paralleltransport stößt man auf das Foucault'sche
Pendel, mit dem 1851 der Nachweis gelang, dass sich die Erde dreht. Aus
physikalischer Sicht
zeugt die Drehung der Schwingungsebene des Pendels nämlich davon, dass das mit der Erde festverbundene Bezugssystem selbst rotiert, also kein Inertialsystem darstellt. Daher treten scheinbar weitere Kräfte auf - hier die Coriolis-Kraft - die das dynamische Verhalten des Pendels aus Sicht eines mit der Erde mitrotierenden Beobachters erklären helfen.
Ein anderes Licht wirft die geometrische Sicht auf das Foucault'sche Pendel: es stellt sich nämlich heraus, dass seine Schwingungsebene parallelverschoben ist entlang der Kurve, die der Aufhängungspunkt des Pendels durch die Erdrotation beschreibt - also entlang eines Breitenkreises. Diesen Effekt möchten wir ausnutzen, um Parallelverschiebung auf beliebigen Flächen zu veranschaulichen. Dazu ersetzen wir die Gravitation, die das Foucault'sche Pendelt veranlasst horizontal zu schwingen, durch eine Zwangskraft, die unserem Modelle nur Drehung in der momentanen Tangentialebene an die Fläche gestattet. Als Beispiel denke man an ein Rad, das auf der Fläche entlang einer beliebigen Kurve bewegt wird, so dass seine Achse stets senkrecht auf der Fläche steht. Dieses mechanische System beschreibt bei geeigneter Anfangsbedingung exakt den Paralleltransport. Diese Ergebniss hat mich veranlasst, eine ausführliche Darstellung der Dynamik starrer Körper aus geometrischer Sicht aufzuschreiben: [Starrerkoerper.pdf]. Unteranderen wird auch die Funktionasweise des Gyrotwisters erklärt
Krümmung und Holonomie:
Der Paralleltransport entlang geschlossener Kurven führt auf zwei wesentliche Begriffe der Differentialgeometrie: Infinitesimal (d.h. für immer kleiner werdende Schleifen) erhält man die Krümmung, während die Transformationen, die durch Paralleltransport entlang beliebiger Schleifen entstehen, die Holonomiegruppe bilden. Daher ist es also im Prinzip möglich, mit obigen Modell die Krümmung und Holonomie einer Fläche experimentel zu bestimmen. Viel wichtiger aber noch erscheint uns die Bemerkung, dass mittels dieses Zugangs auch der Krümmungsbegriff höherdimensionaler Räume plausibel gemacht werden kann.
Geodäten verallgemeinern den Begriff der Geraden in der Euklidischen Geometrie auf gekrümmte Räume. Für Flächen gibt es viele Möglichkeiten, die Geodäten physikalisch zu interpretieren und zu realisieren: als kürzeste Verbindungen zweier Punkte lassen sie sich mit Hilfe eines Gummibands darstellen. Als die am wenigsten gekrümmten Kurven werden sie durch einen Stab verkörpert, der zwischen zwei Kopien der Fläche eingeklemmt ist und als die frontalsten Kurven treten sie in Erscheinung als Linien senkrecht zu einer Wellenfront, bzw. als Weg eines 2-rädrigen Wagens, dessen Räder mit einer starren Achse infinitesimaler Breite verbunden sind. All diese Phänomene geben uns Möglichkeiten an die Hand, physikalisch "gerade" Weg in einer Fläche zu finden, wobei es durchaus erstaunlich ist, dass all diese Phänomene auf denselben Begriff der Geodäte führen:




Parallelverschiebung:
Folgen wir nun beliebigen, also nicht notwendig geradlinigen Wegen in der Ebene, können wir uns trotzdem "merken", welches die ursprüngliche Richtung war, in die wir geschaut haben. Wir wollen sozusagen eine Art Kompass mit uns führen, der die Abweichung vom geraden Weg anzeigt. Geometrisch machen wir dabei nichts anderes als die Anfangsrichtung parallel zu verschieben. Auch auf gekrümmten Flächen kann man den Begriff des Parallelverschiebens einführen und wir suchen, wie im Fall der Geodäten, nach einer intuitiv verständlichen, physikalischen Interpretation. Z.B. kann man den oben erwähnten 2-rädrigen Wagen so abändern, dass man mit ihm auch längs Kurven fahren kann, ein auf ihm montierter Zeiger aber stets die parallelverschobene Richtung anzeigt. Eine solche Zahnradkonstruktion war vermutlich schon dem chinesischen Kaiser Huang-Di vor mehr als 5000 Jahren bekannt. Ein schöner Aufsatz hierzu ist von Prof.D.-E.Liebscher: "Mit dem Kompasswagen über den Globus". In dieser technischen Form wird uns die Paralleverschiebung allerdings niemals in der Natur in Erscheinung treten.
Foucault'sches Pendel und ein ähnliches Rad:
 Auf
der Suche nach einer direkten physikalischen Entsprechung für
den Paralleltransport stößt man auf das Foucault'sche
Pendel, mit dem 1851 der Nachweis gelang, dass sich die Erde dreht. Aus
physikalischer Sicht
Auf
der Suche nach einer direkten physikalischen Entsprechung für
den Paralleltransport stößt man auf das Foucault'sche
Pendel, mit dem 1851 der Nachweis gelang, dass sich die Erde dreht. Aus
physikalischer Sichtzeugt die Drehung der Schwingungsebene des Pendels nämlich davon, dass das mit der Erde festverbundene Bezugssystem selbst rotiert, also kein Inertialsystem darstellt. Daher treten scheinbar weitere Kräfte auf - hier die Coriolis-Kraft - die das dynamische Verhalten des Pendels aus Sicht eines mit der Erde mitrotierenden Beobachters erklären helfen.
Ein anderes Licht wirft die geometrische Sicht auf das Foucault'sche Pendel: es stellt sich nämlich heraus, dass seine Schwingungsebene parallelverschoben ist entlang der Kurve, die der Aufhängungspunkt des Pendels durch die Erdrotation beschreibt - also entlang eines Breitenkreises. Diesen Effekt möchten wir ausnutzen, um Parallelverschiebung auf beliebigen Flächen zu veranschaulichen. Dazu ersetzen wir die Gravitation, die das Foucault'sche Pendelt veranlasst horizontal zu schwingen, durch eine Zwangskraft, die unserem Modelle nur Drehung in der momentanen Tangentialebene an die Fläche gestattet. Als Beispiel denke man an ein Rad, das auf der Fläche entlang einer beliebigen Kurve bewegt wird, so dass seine Achse stets senkrecht auf der Fläche steht. Dieses mechanische System beschreibt bei geeigneter Anfangsbedingung exakt den Paralleltransport. Diese Ergebniss hat mich veranlasst, eine ausführliche Darstellung der Dynamik starrer Körper aus geometrischer Sicht aufzuschreiben: [Starrerkoerper.pdf]. Unteranderen wird auch die Funktionasweise des Gyrotwisters erklärt
Krümmung und Holonomie:
Der Paralleltransport entlang geschlossener Kurven führt auf zwei wesentliche Begriffe der Differentialgeometrie: Infinitesimal (d.h. für immer kleiner werdende Schleifen) erhält man die Krümmung, während die Transformationen, die durch Paralleltransport entlang beliebiger Schleifen entstehen, die Holonomiegruppe bilden. Daher ist es also im Prinzip möglich, mit obigen Modell die Krümmung und Holonomie einer Fläche experimentel zu bestimmen. Viel wichtiger aber noch erscheint uns die Bemerkung, dass mittels dieses Zugangs auch der Krümmungsbegriff höherdimensionaler Räume plausibel gemacht werden kann.
Goldener Schnitt und Fibonacci-Zahlen bei Pflanzen (Phyllotaxis):
Viele Früchte und Blüten bereiten uns nicht nur kulinarisch Freude sondern weisen auch schöne geometrische Muster auf. Besonders auffällig sind dabei Systeme paralleler Spiralen, die augenscheinlich werden, indem man jedes Blatt, Spross etc. mit seinen nächsten Nachbarn verbindet. Zählt man auf diese Art nebeneinanderliegende Spiralen erhält man in der Regel Fibonacci-Zahlen, d.h. Elemente der rekursiven Folge a (n) = a (n-1) + a (n-2) mit den Anfangswerten a (1) = a (2) = 1. Dies ist zunächst verwunderlich und auch das zusätzliche Wissen, dass die Folge der Quotienten a (n)/a (n-1) gegen den goldenen Schnitt konvergiert, macht das Phänomen eher mysteriöser, als dass es zu einer Erklärung beiträgt. Eine naheliegende Hypothese aus der Biologie ist, dass neue Blattsprosse dort entstehen, wo sie am meisten Raum zur Verfügung haben. Dies kann mathematisch modelliert und für eine zylindrische Pflanzen Form auch explizit gelöst werden. Insbesondere stellt sich dabei heraus, dass für das Auftreten von Fibonacci-Zahlen nicht allein die optimale Raumausnutzung verantwortlich ist. Dies alles ist nachzulesen auf der sehr empfehlenswerten Internetseite http://www.math.smith.edu/~phyllo.
Publikationen:
Preprints:
- Pseudo-Riemannian Symmetric Spaces (Diploma-thesis), 2002: [Symmetric-Spaces.pdf]
- Solvable Pseudo-Riemannian Symmetric Spaces, 2003: [math.DG/0301326]
- Normalformen selbst- und schiefadjungierter Operatoren bzgl. einer indefiniten Metrik (in german), 2003: [Normalformen.pdf]
- (joint work with Antonio J. Di Scala and Thomas Leistner), Irreducibly acting subgroups of Gl(n,R), 2005 [math.DG/0507047]



