32428
GESCHICHTE DER MATHEMATIK (D-RE,R; WP-L) R. B¨OLLING
2 SWS VL pro Woche, Di 11-13 Uhr, RUD 25, 1.013
32429
BMS BASIC COURSE "ALGEBRAIC GEOMETRY"
(D-RE,R) G. FARKAS
4 SWS VL pro Woche, Mi 15-17 Uhr, RUD 26, 0'311; Do 11-13 Uhr,
RUD 25, 3.008
- Voraussetzungen:
- Familiarity with commutative algebra.
- Inhalt:
- The course aims to introduce the basic notions and
techniques of algebraic geometry. A sampling to topics to
be discussed include the theory of affine and projective
varieties, Hilbert polynomials and syzygies, sheaves and
an introduction to cohomology.
- Übung:
- 2 SWS pro Woche, Mi 17-19 Uhr, RUD 26, 0'311; G. Farkas
- Literatur:
- Hartshorne: Algebraic geometry.
Mumford: The red book of varietes and schemes.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.401, Tel. 2093-5412
32431
ELLIPTISCHE KURVEN,
MODULFORMEN UND ARITHMETIK (D-RE,R) W. KLEINERT
4 SWS VL pro Woche, Mi 11-13 Uhr, RUD 26, 1'304; Do 15-17 Uhr,
RUD 26, 1'304
- Voraussetzungen:
- Algebra I und II, Grundbegriffe der Algebraischen
Geometrie, der Theorie komplexer Funktionen einer
Variablen, der Topologie und der elementaren
Zahlentheorie.
- Inhalt:
- Analytische Theorie elliptischer Kurven; algebraische
Theorie elliptischer Kurven; arithmetische Theorie
elliptischer Kurven; Modulformen; Eisenstein-Reihen;
modulare Kurven;
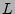 -Reihen; Hecke-Operatoren;
klassische arithmetische Vermutungen (Fermat, Mordell,
Birch & Swinnerton-Dyer, Serre, Hasse, Weil-Taniyama)
und ihr aktueller Entwicklungsstand; Modulprobleme und
Modulräume.
-Reihen; Hecke-Operatoren;
klassische arithmetische Vermutungen (Fermat, Mordell,
Birch & Swinnerton-Dyer, Serre, Hasse, Weil-Taniyama)
und ihr aktueller Entwicklungsstand; Modulprobleme und
Modulräume.
- Übung:
- 2 SWS pro Woche, Do 17-19 Uhr, RUD 25, 3.007; W. Kleinert
- Literatur:
- Hellegouarch, Y.: Invitation to the Mathematics of
Fermat-Wiles. N.Y. 2002.
Milne, J.S.: Elliptic Curves. Kea Books, BookSurge
Publishing, USA, 2006.
Diamond, F.; Shurman, J.: A First Course in Modular
Forms. Springer, 2005
- Sprechstunden:
- Mittwoch, 14-16 Uhr, RUD 25, 1.426, Tel. 2093-1435
32432
TROPICAL ALGEBRAIC
GEOMETRY (D-RE,R) W. GUBLER
4 SWS VL pro Woche, Di 15-17 Uhr, RUD 26, 1'304; Di 17-19 Uhr,
RUD 26, 1'304
- Voraussetzungen:
- Grundkenntnisse in algebraischer Geometrie sind
hilfreich.
- Inhalt:
- Die tropische algebraische Geometrie übersetzt die
algebraische Geometrie in konvexe Geometrie. Dadurch
werden die Probleme substantiell einfacher und man
versucht dann Rückschlüsse auf die algebraische
Geometrie zu machen. In diesem Kurs soll eine Einführung
in diese Problematik gegeben werden. Wir werden auf den
Zusammenhang zu den Gröbnerbasen eingehehen und Methoden
aus der nicht-archimedischen Analysis kennenlernen. Die
Theorie hat vielfältige Anwendungen im Bereich der
Klassischen Geometrie, der algebraischen Geometrie, der
Zahlentheorie, der angewandten Mathematik und sogar der
Informatik.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.418, Tel. 2093-5409
32433
ALGEBRAISCHE SCHNITTTHEORIE (D-RE,R) J. KRAMER
2 SWS VL pro Woche, Mo 11-13 Uhr, RUD 25, 2.009
- Voraussetzungen:
- Algebra I und II
- Inhalt:
- In dieser Spezialvorlesung wird eine Einführung in die
Schnitttheorie algebraischer Kurven gegeben, welche
Ausgangspunkt der algebraischen Schnitttheorie für
höher-dimensionale algebraische Zykeln ist.
- Literatur:
- Fulton, W.: Algebraic Curves. W.A. Benjamin, 1969.
Fulton, W.: Intersection Theory. Springer-Verlag, 1984.
- Geplante Fortsetzung:
- Im Rahmen weiterer Vorlesungen des internationalen
Graduiertenkollegs
Arithmetic and Geometry.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.303, Tel. 2093-5842
32434
EINFüHRUNG IN DIE COMPUTERALGEBRA
(D-RE,R,AN,A; L-VI) A. GRIEWANK
2 SWS VL pro Woche, Mo 09-11 Uhr, RUD 26, 1'304
- Inhalt:
- Fundamental algorithms, Euclidean algorithms and modular
arithmetic continued fractions and Padé approximants.
Fast polynomial multiplication, FFT, Newton on Power
Series, fast linear algebra, factoring and public key
cryptography.
- Übung:
- 1 SWS pro Woche, Mo 11-13 Uhr, 14tgl. (1. Woche), RUD 25,
1.012; L. Lehmann
- Praktikum:
- 1 SWS pro Woche, Mo 11-13 Uhr, 14tgl. (2. Woche), RUD 25,
2.207; L. Lehmann
- Literatur:
- von zur Gothen, J.; Gerhard, J.: Modern Computer Algebra.
Cambridge University Press, ISBN 0521826-462
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.426, Tel. 2093-5820
32435 fällt aus
KOHOMOLOGIE VON GRUPPEN UND ANWENDUNGEN (D-RE,R) V. HEIERMANN
2 SWS VL pro Woche, Di 15-17 Uhr, RD 25, 1.011
32436
TOPOLOGIE II (D-RE,R) [10 SP] TH. FRIEDRICH
2 SWS VL pro Woche, Fr 09-11 Uhr, RUD 25, 1.315
- Inhalt:
- Topologie der Mannigfaltigkeiten.
- Übung:
- 1 SWS pro Woche, Fr 11-13 Uhr, 14tgl. (1. Woche), RUD 25,
1.315; Th. Friedrich
- Sprechstunden:
- Dienstag, 08-09 Uhr, RUD 25, 1.301, Tel. 2093-1628
32437
TOPOLOGISCHE K-THEORIE II
(D-RE,R) TH. FRIEDRICH
2 SWS VL pro Woche, Mo11-13 Uhr, RUD 25, 1.315
- Voraussetzungen:
- Topologische K-Theorie I
- Inhalt:
- Anwendungen der K-Theorie auf Immersionsfragen,
Parallelisierbarkeit der Sphären, Vektorfelder auf
Sphären, Hopf Invariante etc.
- Sprechstunden:
- Dienstag, 08-09 Uhr, RUD 25, 1.301, Tel. 2093-1628
32438
AUSGEWäHLTE METHODEN DER
NICHT-KOMMUTATIVEN GEOMETRIE
(D-RE,R) E. KIRCHBERG
2 SWS VL pro Woche, Do 09-11 Uhr, RUD 25, 1.012
- Voraussetzungen:
- Analysis auf Mannigfaltigkeiten, Funktionalanalysis,
Algebra I
- Inhalt:
- Die Nicht-kommutative Geometrie wurde ca. 1985 von
Alain Connes eingeführt.
Sie stellt Methoden zur Verfügung, die erlauben,
"quantisierte" Räume zu untersuchen.
Anders als im Fall gewöhnlicher Räume sind ihre
Koordinatenalgebren nicht kommutativ und
können daher Phänomene wie z.B. die Heisenbergsche
Unschärfe-Relation modellieren.
Quantisierte Räume treten in vielen Zusammenhängen
auf.
Methoden der Nicht-kommutativen Geometrie können neue
Anwendungen liefern, zum Beispiel
im Bereich der Zahlentheorie (Zugang von Connes zur
Riemannschen Vermutung).
- Übung:
- 2 SWS pro Woche, Do 11-13 Uhr, RUD 25, 1.012; E.
Kirchberg
- Literatur:
- Wird in der Vorlesung bekanntgegeben.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.103, Tel. 2093-1811
32439
OPERATORALGEBREN UND K-THEORIE II
(D-RE,R) E. KIRCHBERG
2 SWS VL pro Woche, Mi 09-11 Uhr, RUD 25, 1.114
- Voraussetzungen:
- Module 1, 2, 5, 6, 7, 15, 19 (bzw. Grundkenntnisse in
Analysis, Funktionalanalysis, Algebra und Topologie)
- Inhalt:
- Zusammenstellung der benötigten Resultate aus K-Theorie,
Kasparovs KK-Gruppen und Ext-Gruppen. Ausblick auf
Anwendungen (Index-Sätze, Novikov-Vermutung,
Klassifikation von Algebren).
- Übung:
- 2 SWS pro Woche, Mi 11-13 Uhr, RUD 25, 1.114; E.
Kirchberg
- Literatur:
- Wird in der Vorlesung bekanntgegeben.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.103, 2093-1811
32440
BMS BASIC COURSE PARTIAL DIFFERENTIAL
EQUATIONS -
HöHERE MATHEMATIK II
(PARTIELLE DIFFERENTIALGLEICHUNGEN (D-RE,R,AN,A) J. SPREKELS
4 SWS VL pro Woche, Do 09-11 Uhr, RUD 25, 1.013; Do 13-15 Uhr,
RUD 25, 1.013
- Voraussetzungen:
- Grundvorlesungen Analysis, BMS Basic Course Functional
Analysis - Höhere Mathematik I (Funktionalanalysis)
- Inhalt:
- Theorie der linearen partiellen Differentialgleichungen:
Typeneinteilung, elementare Lösungsverfahren,
Maximumprinzipien, schwache Lösungen, Sobolev-Räume,
Potentialtheorie, Distributionen.
- Übung:
- 2 SWS pro Woche, Mi 13-15 Uhr, RUD 25, 3.007; J. Heerda
- Literatur:
- Wird in der Vorlesung bekanntgegeben. Es wird ein
Skriptum herausgegeben.
- Sprechstunden:
- Donnerstag, 12-13 Uhr, RUD 25, 2.105, Tel. 2093-5437
32441
FUNKTIONENTHEORIE
(D-RE,R,AN,A; L-I, MA) J. LEITERER
4 SWS VL pro Woche, Mo 15-17 Uhr, RUD 25, 1.013; Mi 13-15 Uhr,
RUD 25, 3.011
- Voraussetzungen:
- Analysis I und II
- Inhalt:
- Im ersten Halbsemester wird eine Einführung in die
Funktionentheorie einer komplexen Veränderlichen gegeben
(bis zum Residuensatz), deren Inhalt identisch ist mit
dem zweiten Halbsemester der Analysis IIIb des
Diplom-Studiengangs. Dieses Halbsemester richtet sich an
Studenten, die bis dahin mindestens Analysis I und II
gehört haben, insbesondere an alle Lehramtsstudenten
nach der Zwischenprüfung. Diplom-Studenten können
dieses erste Halöcht für das Hauptstudium abrechnen.
(Sie könnten es höchstens anstelle des zweiten
Halbsemesters der Analysis IIIb nutzen.) Das zweite
Halbsemester beginnt mit dem Riemannschen Abbildungssatz.
Danach folgt entweder Nevanlinna-Theorie oder ein Beweis
des Primzahlsatzes. Welches der beiden Themen behandelt
wird, ist noch nicht entschieden. Das zweite Halbsemester
richtet sich gleichmaßen an Lehramtsstudenten als auch
an Diplom-Studenten, die diesen Teil für das
Hauptstudium abrechnen können (Vertiefung oder
Spezialisierung).
- Übung:
- 2 SWS pro Woche, Mi 15-17 Uhr, RUD 25, 3.011; J. Leiterer
- Literatur:
- Jedes Lehrbuch über Funktionentheorie einer komplexen
Veränderlichen.
- Sprechstunden:
- Freitag, 13-14 Uhr (bei Bedarf auch länger), RUD 25,
1.420, Tel. 2093-1807
32442 fällt aus
FUNKTIONENTHEORIE II (D-RE,R,AN,A; L-I,III, fak. Physik) I. AGRICOLA
2 SWS VL pro Woche, Mi 11-13 Uhr, RUD 25, 1.012
- Voraussetzungen:
- Grundkenntnisse in Funktionentheorie. Interessenten am
Seminar melden sich bitte im Verlauf der Semesterferien
per e-mail bei mir (je früher, desto besser)
- Inhalt:
- Ausgewählte Themen der komplexen Analysis, basierend auf
der Vorlesung Funktionentheorie I (Complex Analysis I) im
Wintersemester 2007/08. Die Veranstaltung ist sowohl für
Lehramtsstudenten also auch für Diplomstudenten
geeignet.
- Seminar:
- 2 SWS pro Woche, Mi 13-15 Uhr, RUD 25, 1.012; I. Agricola
- Literatur:
- Wird in der Vorlesung bekanntgegeben.
- Sprechstunden:
- Dienstag, 08-09 Uhr, RUD 25, 1.319, Tel. 2093-1822
32443
AUSGEWäHLTE KAPITEL DER FUNKTIONENTHEORIE (D-RE,R) M. BRANDT
2 SWS VL pro Woche, Mo 13-15 Uhr, RUD 25, 1.114
- Voraussetzungen:
- Grundkenntnisse in der Funktionentheorie
- Inhalt:
- Wertannahme holomorpher Funktionen, normale Familien
holomorpher Funktionen, konforme Abbildungen,
Produktdarstellung ganzer und meromorpher Funktionen mit
Anwendung auf spezielle Funktionen.
- Literatur:
- Ahlfors, L.V.: Complex Analysis. McGraw-Hill, Auckland
1985.
- Sprechstunden:
- nach Vereinbarung, Tel. 84185247
32445
BMS BASIC COURSE "DIFFERENTIAL GEOMETRY" -
DIFFERENTIALGEOMETRIE I
(D-RE,R) D. SCHÜTH
4 SWS VL pro Woche, Mo 13-15 Uhr, RUD 26, 1'304; Do 09-11 Uhr,
RUD 26, 1'304
- Voraussetzungen:
- Grundstudium, Analysis und Geometrie auf
Mannigfaltigkeiten
- Inhalt:
- Fortsetzung des Inhalts von Analysis und Geometrie auf
Mannigfaltigkeiten: Fortführung der (semi-)Riemannschen
Geometrie, Variation von Länge und Energie, Krümmung
und Topologie, isometrische Immersionen, Flächentheorie.
-
- http://www.math.hu-berlin.de/~schueth/dg1ss08.html
- Übung:
- 2 SWS pro Woche, Mo 15-17 Uhr, RUD 25, 1.114; M. Weilandt
- Literatur:
- O'Neill: Semi-Riemannian Geometry.
DoCarmo: Riemannian Geometry.
- Geplante Fortsetzung:
- Differentialgeometrie II, WS 2008/09
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.316, Tel. 2093-5864
32450
REELLE ANALYSIS (D-RE,R,AN,A) J. NAUMANN
2 SWS VL pro Woche, Mo 15-17 Uhr, RUD 25, 4.007
- Voraussetzungen:
- Höhere Analysis I und II
- Inhalt:
- Maximal-Funktion von HARDY-LITTLEWOOR. Faltung integrierbarer
Funktionen, Integraloperatoren mit schwach singulären
Kernen.
- Literatur:
- Wird in der Vorlesung bekanntgegeben.
- Geplante Fortsetzung:
- Sobolev-Räume
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.114, Tel. 2093-2239
32451
NICHTLINEARE FUNKTIONALANALYSIS
(D-RE,R,AN,A) J. NAUMANN
4 SWS VL pro Woche, Mo 11-13 Uhr, RUD 25, 1.115; Mi 09-11 Uhr,
RUD 25, 4.007
- Voraussetzungen:
- Höhere Analysis I
- Inhalt:
- Fixpunktsätze von Brouwer und Schauder,
Operatorgleichungen mit monotonen Operatoren, Methode von
Leray-Schauder, Variationsmethoden, nichtlineare
Evolutionsgleichungen.
- Literatur:
- s. homepage
- Geplante Fortsetzung:
- Nichtlineare partielle Differentialgleichungen
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.114, Tel. 2093-2239
32452
NICHTLINEARE PARTIELLE DIFFERENTIALGLEICHUNGEN
(D-AN,A) J. NAUMANN
2 SWS VL pro Woche, Do 11-13 Uhr, RUD 25, 4.007
- Inhalt:
- Grundgleichungen der Hydromechanik, Funktionräume,
schwache Lösungen der Stokes- und
Navier-Stokes-Gleichungen.
- Literatur:
- Wird in der Vorlesung bekanntgegeben.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.114, Tel. 2093-2239
32453
OPTIMALE STEUERUNG
PARTIELLER DIFFERENTIALGLEICHUNGEN
(D-AN,A) O. KLEIN
2 SWS VL pro Woche, Di 15-17 Uhr, RUD 25, 1.012
- Voraussetzungen:
- Lineare Algebra und Analytische Geometrie (Modul 1)
Analysis (Modul 2), Maßtheorie (Modul 6a),
Funktionalanalysis (Modul 15)
- Inhalt:
- Motivierendes Anwendungsproblem: Optimales Heizen.
Wiederholung: Endlichdimensionale Optimierung,
funktionalanalytische Werkzeuge (Sobolev-Räume, Banach-
und Dualräume, schwache Konvergenz). Schwache Lösungen
partieller Differentialgleichungen (PDE). Optimale
Steuerung linearer elliptischer PDE: Existenz- und
Eindeutigkeitssätze, notwendige Optimalitätsbedingungen
(Variationsungleichungen, Differenzierbarkeit in
Banachräumen). Adjungierte Gleichungen. Optimale
Steuerung mit Zustaäml;nkungen. Lagrange-Methode,
Karush-Kuhn-Tucker System. Anwendungbeispiele.
- Literatur:
- Tröltzsch, F.: Optimale Steuerung partieller
Differentialgleichungen. Vieweg Verlag, 2005.
Philip, P.: Optimal Control of Partial Differential
Equations (Skript zur Vorlesung).
- Sprechstunden:
- nach Vereinbarung, WIAS, Tel. 20372-533
32454
REGULARITäTSTHEORIE FüR
NICHTGLATTE PARABOLISCHE PROBLEME (D-RE,R,AN,A) J.A. GRIEPENTROG
2 SWS VL pro Woche, Di 13-15 Uhr, RUD 25, 1.115
- Voraussetzungen:
- Grundstudium Analysis I, II, IIIa, IIIb,
Funktionalanalysis, Evolutionsgleichungen
- Inhalt:
- Parabolische Randwertprobleme zweiter Ordnung mit
nichtglatten Daten, lokale Beschränktheit,
Hölder-Stetigkeit und Positivität schwacher
L&#öngen, globale Eä des parabolischen Operators:
Isomorphismus-Eigenschaft und maximale Regularität in
Sobolev-Morrey-Räumen, Anwendungsbeispiel: Instationäre
Drift-Diffusionsprozesse.
- Sprechstunden:
- nach Vereinbarung, WIAS, Tel. 20372-551
32456
VARIATIONSRECHNUNG UND
OPTIMALE STEUERUNGEN
(D-AN,A) B. KUMMER
4 SWS VL pro Woche, Mi 15-17 Uhr, RUD 25, 1.115; Fr 13-15 Uhr,
RUD 25, 1.013
- Voraussetzungen:
- Analysis I, II, Lineare Algebra und Analytische Geometrie
- Inhalt:
- Variationsrechnung: Aufgabenstellung und Eulersche
Gleichungen, Isoperimetrische Aufgaben,
Transversalitätsbed., variable Randpunkte, Eckenbed. von
Weierstraß und Erdmann; notwendige Beding. bei
Funktionen über Gebieten; Bedingungen zweiter Ordnung
(Legendre, Jacobi), starke, schwache Lösungen.
Optimale Steuerungen: Aufgabenstellungen und -typen,
Regularitätsbed. und Strafansätze, Lagrange Bed.,
adjungiertes Systemäunktion; grundlegende Abschätzungen
und Pontrjagins Maximumprinzip, Transversalitätsbed. und
variable Endzeit; spezielle Aufgaben: lineare Probleme,
Sprünge, Feedback; Inklusionen 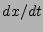 in
in 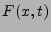 .
.
Zusammenhänge: Steuerungsaufgaben - Variationsaufgaben -
dynamische Optimierung; Ansätze für Lösungsmethoden.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.408, Tel. 2093-5844
42458
BMS BASIC COURSE NONLINEAR OPTIMIZATION -
NICHTLINEARE OPTIMIERUNG (D-AN,A) A. GRIEWANK
4 SWS VL pro Woche, Do 11-13 Uhr, RUD 25, 1.115; Do 15-17 Uhr,
RUD 25, 1.013
- Voraussetzungen:
- Analysis I, II, Lineare Algebra und Analytische Geometrie
I, II. Linear Programming desirable/erwünscht
- Inhalt:
- Classification of Optimization problems, unconstrained
optimization by descent with line-search. Nonlinear least
squares. Optimality conditions for constrained problems.
Successive quadratic programming. Quasi-Newton methods.
Convergence rates, complexity extimates.
- Übung:
- 2 SWS pro Woche, Mi 11-13 Uhr, RUD 25, 3.011; E. Özkaya
- Literatur:
- Bonnans, F. et al.: Numerical Optimization. Springer,
ISBN 9783540354451.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.426, Tel. 2093-5820
32461
STOCHASTISCHE OPTIMIERUNG (D-AN,A) W. RöMISCH
2 SWS VL pro Woche, Mo 15-17 Uhr, RUD 25, 3.011
- Voraussetzungen:
- Stochastik I, möglichst auch Optimierung I
- Inhalt:
- Erwartungswertfunktionale, zweistufige stochastische
Optimierung, Optimalität, Dualität, ganzzahlige
stochastische Optimierung, mehrstufige stochastische
Optimierung, Lösungsverfahren, Diskretisierung,
Dekomposition.
- Literatur:
- Ruszczynski; Shapiro (eds.): Stochastic Programming.
Handbook OR and Man. Sci., Elsevier, 2003.
- Sprechstunden:
- Mittwoch, 13-15 Uhr, RUD 25, 2.414, Tel. 2093-2561
32463
NUMERISCHE BEHANDLUNG
VON PARTIELLEN DIFFERENTIALGLEICHUNGEN II
(D-AN,A) C. CARSTENSEN,
A. SCHRöDER
4 SWS VL pro Woche, Di 13-15 Uhr, RUD 25, 1.013; Mi 11-13 Uhr,
RUD 25, 1.115
- Inhalt:
- Die Vorlesung setzt die entsprechende Lehrveranstaltung
des Wintersemesters 2007/08 mit speziellen Kapiteln fort.
Die im ersten Teil erlernten Techniken zur Approximation
partieller Differentialgleichungen sollen auf Probleme
aus der Elastizitäts- und Strömungstheorie angewendet
und dabei vertieft werden. Zusätzlich werden andere
Konzepte wie Randelementemethode und Mehrgitterverfahren
diskutiert. äg mit Übung und Praktikum ist zukünftigen
Kandidaten/innen für Diplomarbeiten in der Numerik von
partiellen Differentialgleichungen dringend empfohlen.
- Übung:
- 2 SWS pro Woche, Mi 13-15 Uhr, RUD 25, 3.006; N.N.
- Praktikum:
- 2 SWS pro Woche, Mi 15-17 Uhr, RUD 25, 2.207; N.N.
(fakultativ)
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.411, Tel 2093-5844
32464
MATHEMATISCHE MODELLIERUNG (D-AN,A) P. EVANS
2 SWS VL pro Woche, Fr 09-11 Uhr, RUD 25, 1.114
- Voraussetzungen:
- Grundvorlesung Analysis, Lineare Algebra und Analytische
Geometrie, Numerik oder äquivalent
- Inhalt:
- An introduction to fundamental ideas from mathematical
modelling: scaling, self-similarity, dynamical systems
and the simplification and interpretation of solutions.
Application areas may include biology (e.g. predator-prey
models) fluid mechanics (e.g. thin liquid films
exhibiting shocks and instabilities) or other areas
depending on the interests of participants.
- Übung:
- 1 SWS pro Woche, Fr 11-13 Uhr, 14tgl. (1. Woche), RUD 25,
1.114; P. Evans
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.101, Tel. 2093-5432
32465
OPTIMIERUNGSPROBLEME
MIT WAHRSCHEINLICHKEITSRESTRIKTIONEN
(D-AN,A) R. HENRION
2 SWS VL pro Woche, Do 09-11 Uhr, RUD 25, 1.114
- Voraussetzungen:
- Grundvorlesung Optimierung und Stochastik
- Inhalt:
- Optimierungsprobleme mit Zufallsparametern, Modelle,
Struktur (Stetigkeit, Differenzierbarkeit, Konvexität),
Numerik, Anwendung auf praktische Probleme.
- Literatur:
- Prékopa, A.: Stochastic Programming. Kluwer, Dordrecht
1995.
- Sprechstunden:
- Donnerstag, 13 Uhr, WIAS, Tel. 20372-540
32466
STATISTIK II (D-AN,A) N.N.
2 SWS VL pro Woche, Mi 09-11 Uhr, RUD 26, 1'304
- Inhalt:
- Wird zu gegebener Zeit bekanntgegeben.
- Übung:
- 1 SWS pro Woche, Mi 11-13 Uhr, 14tgl. (1. Woche), RUD 25,
3.008; N.N.
32468
REGRESSIONS- UND VARIANZANALYSE (D-AN,A) [10
SP] R. THRUM
4 SWS VL pro Woche, Di 11-13 Uhr, RUD 25, 1.115; Fr 11-13 Uhr,
RUD 25, 1.115
- Inhalt:
- Grundlagen der Mathematischen Statistik, Schätz- und
Testverfahren in linearen Modellen, optimale
Versuchsplanung und Vorhersage in der Regressionsanalyse,
Modelle und Hypothesenprüfung der Varianzanalyse (ANOVA
+ MANOVA), Zeitreihenanalyse.
- Übung:
- 2 SWS pro Woche: Di 13-15 Uhr, RUD 25, 2.009; R. Thrum
- Literatur:
- Monographien von G. Seber, Ferguson, C.R. Rao, Humak I
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.207, Tel. 2093-5838
32469
ZUVERL"ASSIGKEITSTHEORIE
(D-AN,A; L-V; BA, MA Statistik) B. GERLACH
3 SWS VL pro Woche, Di 09-11 Uhr, RUD 25, 1.114; Mi 13-15 Uhr,
14tgl. (1. Woche), RUD 25, 1.114
- Voraussetzungen:
- Grundkurs Stochastik
- Inhalt:
- Basierend auf dem Grundkurs Wahrscheinlichkeitstheorie
gibt die Lehrveranstaltung einen Überblick über die
grundlegenden Verfahren der (probabilistischen)
Zuverlässigkeitsanalyse, die nicht nur in der Technik,
sondern auch in anderen Disziplinen, Anwendung finden.
Aufbauend auf einem Basiswissen in
Wahrscheinlichkeitstheorie werden grundlegende Kenntnisse
der Stochastik an einem konkreten Gegenstand vertieft.
Die Übungen dienen dem Training praktischer Fähigkeiten
auf dem Gebiet der Wahrscheinlichkeitsrechnung anhand
praktisch relevanter Beispiele. Hierbei wird die
Erfahrung aus verschiedenen Industrieverträgen genutzt.
I. Analytische Methoden.
Grundbegriffe der Zuverlässigkeitstheorie:
Lebensdauerverteilungen, Überlebenswahrscheinlichkeit,
MTBF-Wert, Ausfallrate. Zuverlässigkeitsberechnungen von
Systemen: Modelle und wesentliche Beispiele, Redundanz,
modulare Zerlegung, Fehlerbaumanalysen, Wichtigkeiten
für Komponenten, exakte und Näherungsmethoden.
Abschätzungen, Fallstudie. Lebensdauerverteilungen von
Komponenten und Systemen: Parametrische Familien von
Lebensdaueäerteilungen (Exponential-Weibull-Gamma- und
logarithmische Normalverteilung). Grundlegende Begriffe
deäAlterung, Näherungen und Abschätzungen.
II. Statistische Verfahren für Betriebsdaten.
Problemstellung, Stichproben. Prüfpläne, zensierte
Daten. Anpassung einer Lebensdauerverteilung an
vorliegende Daten: Grafische Verfahren, Anpassungstests.
Schätzverfahren: Parameterschätzungen und
Konfidenzintervalle bei wichtigen
Lebensdauerverteilungen.
- Übung:
- 1 SWS pro Woche, Mi 13-15 Uhr, 14tgl. (2. Woche), RUD 25,
1.114; B. Gerlach
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.219, Tel. 2093-5812
32470
VERSICHERUNGSMATHEMATIK I (D-AN,A) B. GERLACH, A.V. SCHAAFFHAUSEN
4 SWS VL pro Woche, Do 11-13 Uhr, RUD 26, 1'304; Fr 09-11 Uhr,
RUD 25, 1.115
- Inhalt:
- Die Vorlesung wendet sich an Studenten der Mathematik und
Wirtschaftsmathematik, sowie mathematisch interessierte
Studenten der Wirtschaftswissenschaften. Vermittelt
werden grundlegende Begriffe der Versicherungsmathematik,
insbesondere auf den Gebieten Lebens- und
Pensionsversicherungen. Dabei werden Grundkenntnisse der
Mathematik, der Wahrscheinlichkeitstheorie und der
Mathematischen Statistik (Grundkurs Stochastik)
vorausgesetzt. Folgende Schwerpunkte werden behandelt:
Versicherungsprozesse (Prämien, Leistungen, Optionen,
Beispiele); Verzinsung (Grundbegriffe, einfache Modelle);
allgemeine Wertentwicklung eines Fonds; Renten;
Nettoprämien und Nettodeckungskapital;
Kommutationszahlen; ausreichende Prämie und
ausreichendes äckungskapital; verschiedene
Ausscheideursachen, Pensionsversicherungeä Satz von
Cantelli; Versicherung auf mehrere Leben;
Überschußzerlegung und Überschußabrechnung.
Der Kurs wird im Rahmen der Grundstudienrichtung
Mathematik als Teil der Nebenfachausbildung in
Wirtschaftswissenschaften akzeptiert.
- Übung:
- 2 SWS pro Woche, Do 15-17 Uhr, RUD 25, 3.007; B. Gerlach,
A.v. Schaaffhausen
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.219, Tel. 2093-5812
32471
BMS BASIC COURSE STOCHASTIC PROCESSES II: CONTINUOUS TIME -
STOCHASTISCHE ANALYSIS (D-AN,A) [10 SP] U. KüCHLER
4 SWS VL pro Woche, Do 09-11 Uhr, RUD 26, 0'311; Do 13-15 Uhr,
RUD 26, 0'310
- Inhalt:
- Brownian Motion, Martingales, Semimartingales, stochastic
integrals, Itô's formula, stochastic differential
equations, Girsanovs theorem, Lévy processes,
applications to Mathematical Finance.
- Übung:
- 2 SWS pro Woche, Mi 11-13 Uhr, RUD 25, 4.007; I. Penner
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.203, Tel. 2093-5851
32472
STATISTIK STOCHASTISCHER PROZESSE (D-AN,A) U. KüCHLER
2 SWS VL pro Woche, Mi 13-15 Uhr, RUD 26, 1'304
- Inhalt:
- Die Statistik stochastischer Prozesse muß ohne die
klassische Voraussetzung unabhängiger identisch
verteilter Zufallsgrößen als Bestandteile einer
Stichprobe auskommen. In der Vorlesung werden Methoden
vorgestellt, die dennoch wirksames Schätzen von
Parametern und Testen von Hypothesen ermöglichen
(Likelihoodtheorie, Pseudolikelihood, Schätzfunktion auf
Martingalbasis, EM-Algorithmus, Filterungstheorie, Change
point detection). Einbezogen werden unterschiedliche
Proäusionen, Punktprozesse, Lévyprozesse, Markovsche
Ketteöa. in Finanz- und Versicherungsmarktmodellen
illustrieren den Stoff.
- Übung:
- 1 SWS pro Woche, Mi 15-17 Uhr, 14tgl. (1. Woche), RUD 26,
1'304; I. Penner
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.203, Tel. 2093-5851
32473 fällt aus
MARKOVSCHE PROZESSE - THEORIE UND ANWENDUNGEN
(D-AN,A) N.N.
2 SWS VL pro Woche, Mo 09-11 Uhr, RUD 25, 1.115
32477
MATHEMATISCHE LOGIK II
(D-RE,R) H.-P. TUSCHIK
4 SWS VL pro Woche, Mo 13-15 Uhr, RUD 25, 1.115; Di 11-13 Uhr,
RUD 25, 1.011
- Voraussetzungen:
- Logik I oder Grundkenntnisse aus einer in die
mathematische Logik einführenden Vorlesung
- Inhalt:
- Es werden grundlegende Begriffe, Methoden und Ergebnisse
der klassischen Modelltheorie behandelt.
- Literatur:
- Wird in der Vorlesung angegeben.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.404, Tel. 2093-5867
32478
EINFüHRUNG IN DIE
AXIOMATISCHE MENGENLEHRE
(D-RE,R) H.-P. TUSCHIK
2 SWS VL pro Woche, Fr 13-15 Uhr, RUD 25, 1.115
- Voraussetzungen:
- Grundkenntnisse in mathematischer Logik
- Inhalt:
- Mengenlehre als Grundlage für die Mathematik, allgemein
akzeptierte Axiome, Erweiterungen, Unabhängigkeiten,
Beweismethoden.
- Literatur:
- Wird in der Vorlesung angegeben.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.404, Tel. 2093-5867
32479
ALGEBRA/ZAHLENTHEORIE (L-IV, BA) W. GUBLER
4 SWS VL pro Woche, Mo 13-15 Uhr, RUD 26, 0'311; Mi 09-11 Uhr,
RUD 26, 0'310
- Voraussetzungen:
- Lineare Algebra und Analytische Geometrie I
- Inhalt:
- Klassische und algebraische Grundlagen der elementaren
Zahlentheorie, systematischer Aufbau der Zahlbereiche,
Algebra und Arithmetik in Restklassenringen ganzer
Zahlen.
- Übungen:
- 2 SWS pro Woche:
UE 1: Mo 15-17 Uhr, RUD 26, 0'311; P. Bannasch
UE 2: Mi 11-13 Uhr, RUD 26, 0'311; C. Christensen
- UE 3: Mi 15-17 Uhr, RUD 25, 1.114; E.L. Wirl
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.418, Tel. 2093-5409
32480
ALGEBRA/ZAHLENTHEORIE UND IHRE DIDAKTIK (BA) J. KRAMER
1 SWS VL pro Woche, Mi 13-15 Uhr, 14tgl. (1. Woche), RUD 26,
0'310
- Voraussetzungen:
- Lineare Algebra und Analytische Geometrie I
- Inhalt:
- Herstellung didaktischer Bezüge zu arithmetischen
Inhalten des Mathematikunterrichts, insbesondere zur
Vorgehensweise bei der Erweiterung der Zahlbereiche in
der Schule.
- Übung:
- 1 SWS pro Woche, Mi 13-15 Uhr, 14tgl. (2. Woche), RUD 26,
0'310; K. Klembalski
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.303, Tel. 2093-5842
32481
fällt aus
AUSGEWäHLTE KAPITEL ZUR ALGEBRA/ZAHLENTHEORIE
(L) J. KRAMER
2 SWS VL pro Woche, Mo 09-11 Uhr, RUD 25, 1.012
- Inhalt:
- Konstruktion mit Zirkel und Lineal, Algebraizität und
Transzendenz, symmetrische Polynome und Funktionen,
Unmöglichkeit der Lösbarkeit der Gleichung 5. Grades in
Radikalen.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.303, Tel. 2093-5842
32482
VERTIEFUNGSKURS NUMERISCHE MATHEMATIK (L-VI) H.-D. NIEPAGE
2 SWS VL pro Woche, Di 11-13 Uhr, RUD 26, 1'304
- Voraussetzungen:
- Grundkurs Numerische Mathematik (Lehramt)
- Inhalt:
- Ergänzende und vertiefende Aussagen zu Themen des
Grundkurses Numerische Mathematik. Einführung zu
Lösungsverfahren für gewöhnliche
Differentialgleichungen.
- Literatur:
- Wird in der Vorlesung bekanntgegeben.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 4.005, Tel. 2093-2353
32486
fällt aus
VERTIEFENDES WAHLGEBIET:
GEWöHNLICHE DIFFERENTIALGLEICHUNGEN (L,
MA) D. KNEES
4 SWS VL pro Woche, Mo 11-13 Uhr, RUD 25, 4.007; Mi 11-13 Uhr,
RUD 26, 0'311
- Voraussetzungen:
- Lineare Algebra und Analytische Geometrie I, II, Analysis
I, II
- Inhalt:
- Beispiele gewöhnlicher Differentialgleichungen in
Naturwissenschaften und Technik; analytische
Lösungsmethoden; Existenz- und Eindeutigkeitssätze;
stetige Abhängigkeit von Anfangsbedingungen und
Parametern; lineare Systeme, Stabilität.
- Übung:
- 2 SWS pro Woche, Mo 13-15 Uhr, RUD 25, 4.007; D. Knees
- Literatur:
- Aulbach, B.: Gewöhnliche Differentialgleichungen.
Spektrum Akademischer Verlag.
Amann, H.: Gewöhnliche Differentialgleichungen. de
Gruyter, Berlin.
Walter, W.: Gewöhnliche Differentialgleichungen.
Springer-Verlag.
- Sprechstunden:
- nach Vereinbarung, WIAS, Tel. 20372-552
hpt 2008-06-13