(32428)
ALGEBRA II (D-RE,R) W. KLEINERT
4 SWS VL pro Woche, Mi 11-13 Uhr, RUD 26, 0'311; Fr 11-13 Uhr,
RUD 26, 1'304
- Voraussetzungen:
- Lineare Algebra und Analytische Geometrie I, II, Algebra
I
- Inhalt:
- Gemäß Modulbeschreibung (Amtl. Mitteilungsblatt der HU,
Nr. 19/2004, S.14)
Elemente der kommutativen Algebra: spezielle Ringe und
Moduln; Ringerweiterungen und Galois-theorien; Elemente
der kategoriellen und homologischen Algebra; multilineare
Algebra und Anwendungen; Algebren und Elemente der
affinen algebraischen Geometrie; Elemente der
Invariantentheorie; Matrix-Algebren und Darstellungen.
- Übungen:
- 2 SWS pro Woche:
Fr 13-15 Uhr, RUD 26, 1'304; W. Kleinert
- Literatur:
- [1] Jantzen, J.C.; Schwermer, J.: Algebra.
Springer-Verlag, Berlin 2005.
[2] Grillet, P.: Algebra. Wiley & Sons, New York
1999.
[3] Douady, A. et R.: Algèbre et théories galoisiennes.
Cassini, Paris 2005.
- Geplante Fortsetzung:
- SS 2007, Einführung in die algebraische Geometrie (4+2
SWS)
- Sprechstunden:
- Mittwoch, 14-16 Uhr, RUD 25, 1.426, Tel. 2093-1435
(32431)
HÖHERE ANALYSIS I
(FUNKTIONALANALYSIS) (D-RE,AN,R,A) E. KIRCHBERG
4 SWS VL pro Woche, Mo 11-13 Uhr, RUD 26, 0'311; Fr 09-11 Uhr,
RUD 25, 1.115
- Voraussetzungen:
- Lineare Algebra und Analytische Geometrie I, II, Analysis
I-IV
- Inhalt:
- Normierte Vektorräume, Sätze von Hahn-Banach und
Banach-Steinhaus, Hilbert-Räume, kompakte Operatoren,
Fredholm-Operatoren, Index, abgeschlossene und
beschränkte Operatoren, Resolvente und Spektrum,
Spektraltheorie selbstadjungierter und normaler
Operatoren, Integraloperatoren, Fourier- und
Laplace-Transformationen.
- Übungen:
- 2 SWS pro Woche:
Mo 13-15 Uhr, RUD 25, 3.006; E. Kirchberg
- Literatur:
- Hirzebruch; Scharlau: Einführung in die
Funktionalanalysis. Spektrum Verlag.
Meise; Vogt: Einführung in die Funktionalanalysis.
Vieweg.
Pedersen, G.K.: Analysis Now. Springer, 1989.
Alt: Lineare Funktionalanalysis. Springer.
- Geplante Fortsetzung:
- Höhere Analysis II (Partielle Differentialgleichungen)
- Sprechstunden:
- Donnerstag, 14-16 Uhr, RUD 25, 1.103, Tel. 2093-1811
(32432)
BMS BASIC COURSE ,,COMPLEX ANALYSIS`` -
FUNKTIONENTHEORIE (D-RE,R; L-I) J. LEITERER
4 SWS VL pro Woche, Mo 09-11 Uhr, RUD 25, 3.006; Mi 09-11 Uhr,
RUD 26, 0'311
- Voraussetzungen:
- Lineare Algebra und Analytische Geometrie I, II, Analysis
I, II
- Inhalt:
- Im ersten Halbsemester wird eine Einführung in die
Funktionentheorie einer komplexen Veränderlichen gegeben
(bis zum Residuensatz), deren Inhalt identisch ist mit
dem zweiten Halbsemester der Analysis IV des
Diplom-Studiengangs. Dieses Halbsemester richtet sich an
Studenten, die bis dahin mindestens Analysis I und II
gehört haben, insbesondere an alle Lehramtsstudenten
nach der Zwischenprüfung. Diplom-Studenten können
dieses erste Halbsemester nicht für das Hauptstudium
abrechnen. (Sie könnten es höchstens anstelle des
zweiten Halbsemesters der Analysis IV nutzen.)
Im zweiten Halbsemester werden der Primzahlsatz und der
Riemannsche Abbildungssatz behandelt. Es richtet sich
gleichermaßen an Lehramtsstudenten als auch an
Diplom-Studenten, die diesen Teil für das Hauptstudium
abrechnen können (Vertiefung oder Spezialisierung).
Im Sommersemester folgt eine Fortsetzung als 2-stündige
Vorlesung mit dazugehörigem Seminar, die ebenfalls
sowohl für das Lehramt als auch das Diplom geeignet ist.
- Übungen:
- 2 SWS pro Woche:
Mi 11-13 Uhr, RUD 25, 3.011; J. Leiterer
- Literatur:
- Jedes der vielen Bücher über Funktionentheorie, z.B.
Jänich: Funktionentheorie. Springer-Lehrbuch.
Freitag; Busam: Funktionentheorie. Springer-Lehrbuch.
Remmert: Funktionentheorie 1. Springer-Lehrbuch.
- Geplante Fortsetzung:
- SS 2007, VL ,,Ausgewählte Kapitel der
Funktionentheorie`` (2 SWS) mit dazugehörigem Seminar (2
SWS)
- Sprechstunden:
- Freitag, 13-15 Uhr, RUD 25, 1.420, 2093-1807
(32433)
QUANTENFELDTHEORIE FÜR MATHEMATIKER II
(D-RE,R) J. BRÜNING
4 SWS VL pro Woche, Mo 15-17 Uhr, RUD 25, 1.013; Mi 13-15 Uhr,
RUD 25, 3.007
- Voraussetzungen:
- Vordiplom, Analysis auf Mannigfaltigkeiten, möglichst
auch höhere Analysis I & II
- Literatur:
- Wird in der Vorlesung angegeben; Lehrbücher, die dem
Ziel entsprechen, gibt es nicht.
- Sprechstunden:
- Mittwoch, 15-16 Uhr, RUD 25, 1.314, Tel. 2093-2522
(32435)
BMS BASIC COURSE ,,ANALYSIS AND GEOMETRY ON
MANIFOLDS`` -
ANALYSIS UND GEOMETRIE AUF MANNIGFALTIGKEITEN (D-RE,R) K. MOHNKE
4 SWS VL pro Woche, Do 09-11 Uhr, RUD 25, 1.013; Do 13-15 Uhr,
RUD 26, 1'304
- Voraussetzungen:
- Analysis I, II, IIIa, IIIb (Modul 2, 5, 6) (wobei es
genügt, Analysis IIIa parallel zu hören), Lineare
Algebra und Analytische Geometrie I, II (Modul 1)
- Inhalt:
- Differenzierbare Mannigfaltigkeiten, Differentialformen,
Satz von Stokes, Einführung in die Riemannsche
Geometrie.
- Übungen:
- 2 SWS pro Woche:
Mi 09-11 Uhr, RUD 25, 3.006; K. Mohnke
- Literatur:
- Warner, F.: Foundations of Differentiable Manifolds and
Lie Groups. Springer, 1996
Guillemin, V.; Pollack, A.: Differential Topology.
Prentice-Hall, 1974.
DoCarmo, M.: Riemannian Geometry. Birkhäuser, 1993.
- Geplante Fortsetzung:
- SS 2007 od. WS 2007/08 Differentialgeometrie I
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.306, Tel. 2093-1814
(32438)
DIFFERENTIALGEOMETRIE III (D-RE,R) TH. FRIEDRICH
4 SWS VL pro Woche, Mo 09-11 Uhr, RUD 25, 3.011; Mi 09-11 Uhr,
RUD 25, 1.115
- Voraussetzungen:
- Vordiplom, Differentialgeometrie I, II
- Inhalt:
- Dirac-Operatoren, spezielle Geometrien, metrische
Zusammenhänge mit Torsion, Lösungen der Gleichungen der
String-Theorie.
- Übungen:
- 2 SWS pro Woche:
Mo 11-13 Uhr, RUD 25, 3.011; Th. Friedrich
- Sprechstunden:
- Dienstag, 08-09 Uhr, RUD 25, 1.301, 2093-1628
(32442)
SOBOLEV-RÄUME (D-RE,AN,R,A) J. NAUMANN
2 SWS VL pro Woche, Di 11-13 Uhr, RUD 25, 1.013
- Voraussetzungen:
- Maß- und Integrationstheorie, Funktionalanalysis
- Inhalt:
- Geschichtliche Entwicklung, schwache Ableitung und ihre
Eigenschaften, SOBOLEV-Raum
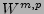 ,
Eigenschaften von SOBOLEV-Funktionen,
Einbettungssätze, einige Anwendungen auf partielle
Differentialgleichungen.
,
Eigenschaften von SOBOLEV-Funktionen,
Einbettungssätze, einige Anwendungen auf partielle
Differentialgleichungen.
- Literatur:
- Wird in der Vorlesung bekanntgegeben.
- Geplante Fortsetzung:
- keine
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.114, Tel. 2093-2239
(32443) fällt aus
FUNKTIONENRÄUME
(D-RE,AN,R,A) J. NAUMANN
2 SWS VL pro Woche, Fr 13-15 Uhr, RUD 25, 2.009
- Voraussetzungen:
- Maß- und Integrationstheorie, Funktionalanalysis
- Inhalt:
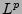 -Räume
(ergänzende Kapitel), LORENTZ-Räume,
ORLICZ-Räume, Raum BMO.
-Räume
(ergänzende Kapitel), LORENTZ-Räume,
ORLICZ-Räume, Raum BMO. - Literatur:
- Wird in der Vorlesung bekanntgegeben.
- Geplante Fortsetzung:
- keine
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.114, Tel. 2093-2239
(32444)
BMS BASIC COURSE ,,PARTIAL DIFFERENTIAL EQUATIONS`` -
HÖHERE ANALYSIS II (D-RE,AN,R,A) J. NAUMANN
4 SWS VL pro Woche, Do 11-13 Uhr, RUD 25, 1.013; Do 15-17 Uhr,
RUD 25, 1.115
- Voraussetzungen:
- Lineare Algebra und Analytische Geometrie I, II (Modul
1), Analysis I, II (Modul 2), Analysis IIIa (Modul 5),
Analysis IIIb (Modul 6), Höhere Analysis I (Modul 15)
- Inhalt:
- Typen linearer partieller Differentialgleichungen,
Grundlösungen, Distributionen, SOBOLEV-Räume, Existenz
und Eindeutigkeit schwacher Lösungen elliptischer
Randwertprobleme, desgleichen schwacher Lösungen
parabolischer und hyperbolischer
Rand-Anfangswertprobleme.
- Übungen:
- 2 SWS pro Woche:
Mi 13-15 Uhr, RUD 25, 3.006; N.N.
- Literatur:
- Wird in der Vorlesung bekanntgegeben.
- Geplante Fortsetzung:
- keine
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.114, Tel. 2093-2239
(32448)
OPTIMALE STEUERUNG BEI
PARABOLISCHEN DIFFERENTIALGLEICHUNGEN
(D-AN,A; L-I,VI) A. GLITZKY
2 SWS VL pro Woche, Fr 09-11 Uhr, RUD 25, 1.011
- Voraussetzungen:
- Grundkurs Analysis I-IV, Funktionalanalysis, parabolische
Differentialgleichungen
- Inhalt:
- Am Beispiel einfacher Optimalsteuerprobleme mit
gewöhnlichen Differentialgleichungen erläutern wir die
Grundbegriffe der optimalen Steuerung und motivieren
typische Fragestellungen. Wir untersuchen
Optimalsteuerprobleme mit parabolischen
Differentialgleichungen, beginnen dabei mit linearen
Kontrollsystemen und betrachten danach ausgewählte
nichtlineare Probleme. Wir stellen Methoden aus der
konvexen Analysis zur Lösung von Minimumproblemen (unter
Nebenbedingungen) und benötigte Aussagen aus der Theorie
partieller Differentialgleichungen bereit. Die
wesentlichen Inhalte der Vorlesung betreffen Existenz-
und Einzigkeitsaussagen, Optimalitätsbedingungen und
Steuerbarkeitsaussagen.
- Literatur:
- Lions, J.L.: Optimal Control of Systems Governed by
Partial Diff. Equations. Berlin 1971.
Neittaanmäki, P.; Tiba, D.: Optimal Control of Nonlinear
Parabolic Systems. 1994.
Tröltzsch, F.: Optimality Conditions for Parabolic
Control Problems and Applications. Leipzig 1984.
Weitere Literatur wird in der Vorlesung bekanntgegeben.
- Geplante Fortsetzung:
- keine
- Sprechstunden:
- nach Vereinbarung, WIAS, Tel. 20372-568
(32449)
NUMERIK GEWÖHNLICHER
DIFFERENTIALGLEICHUNGEN
(D-AN,A) W. RÖMISCH
4 SWS VL pro Woche, Mi 11-13 Uhr, RUD 25, 1.115; Fr 11-13 Uhr,
RUD 25, 1.115
- Übungen:
- 2 SWS pro Woche:
Fr 13-15 Uhr, RUD 25, 3.008; N.N.
- Sprechstunden:
- Mittwoch, 13-15 Uhr, RUD 25, 2.414, Tel. 2093-2561
(32450)
NUMERIK PARTIELLER
DIFFERENTIALGLEICHUNGEN
(D-AN,A) C. CARSTENSEN, J. GEISER
4 SWS VL pro Woche, Mi 13-15 Uhr, RUD 25, 1.013; Do 13-15 Uhr,
RUD 25, 1.013
- Voraussetzungen:
- Lineare Algebra und Analytische Geometrie I, II (Modul
1), Gewöhnliche Differentialgleichungen (Teilmodul 5b),
Numerische Mathematik I (Modul 9), Höhere Analysis I, II
(Modul 15, 16)
- Inhalt:
- Klassische Lösungen und Differenzenverfahren für
elliptische Differentialgleichungen; elliptische
Variationsgleichungen und deren konforme Approximation;
Galerkin-Verfahren; Methode der finiten Elemente;
Gittergenerierung; Fehlerabschätzung; Konvergenz;
Lösung der diskreten Probleme; Mehrgittermethoden;
Linies-Methode und Rothe-Methode für parabolische
Differentialgleichungen.
- Übungen:
- 2 SWS pro Woche:
Mi 15-17 Uhr, RUD 25, 2.009; S. Bartels, R. Müller.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.406, Tel. 2093-5844
(32451)
THEORIE UND NUMERIK C. CARSTENSEN
VON INTEGRALGLEICHUNGEN
(D-AN,A) S. BARTELS, J. GEISER
4 SWS VL pro Woche, Di 13-15 Uhr, RUD 26, 1'304; Do 09-11 Uhr,
RUD 25, 3.011
- Inhalt:
- Theorie: Riesz-Schauder-Theorie, klassische und
Hölder-stetige Funktionen, Existenz- und
Eindeutigkeitsaussagen.
Numerik: Volterrasche und Fredholmsche
Integralgleichungen werden behandelt, Randelementmethoden
und Kernapproximationen als Diskretisierung, Konvergenz-
und Fehleranalysis präsentiert.
- Übungen:
- 2 SWS pro Woche:
Do 11-13 Uhr, RUD 25, 3.011; N.N.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.406, Tel. 2093-5844
(32453)
NUMERIK DER
STOCHASTISCHEN OPTIMIERUNG
(D-AN,A) W. RÖMISCH
4 SWS VL pro Woche, Mo 15-17 Uhr, RUD 26, 0'311; Do 15-17 Uhr,
RUD 26, 1'304
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.414, Tel. 2093-2561
(32455)
NUMERISCHE VERFAHREN
IN DER VERSICHERUNGSMATHEMATIK
(D-AN,A) E. BUCKWAR
2 SWS VL pro Woche, Mo 11-13 Uhr, RUD 25, 1.114
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.217, Tel. 2093-5889
(32457)
ab 23.10.2006
VARIATIONSUNGLEICHUNGEN
UND IHRE ANWENDUNGEN
(D-AN,A) B. KUMMER
2 SWS VL pro Woche, Mo 13-15 Uhr, RUD 25, 1.114
- Voraussetzungen:
- Grundkurse Analysis und Lineare Algebra und Analytische
Geometrie
- Inhalt:
- Grundlegende Begriffe (Normalenkegel, Subdifferentiale),
Zusammenhänge und Rechenregeln; Existenzaussagen,
Beziehungen zu Fixpunkten und Ekeland-Prinzip; spezielle
Variationsungleichungen für Multilevel-Optimierung,
Gleichgewichtsprobleme und MPEC's; Lösungsverfahren.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.408, Tel. 2093-5844
(32458)
ab 24.10.2006
OPTIMIERUNG I (D-AN,A) B. KUMMER
4 SWS VL pro Woche, Di 11-13 Uhr, RUD 25, 1.115; Do 15-17 Uhr,
RUD 25, 1.013
- Voraussetzungen:
- Lineare Algebra u. Analytische Geometrie I, II (Modul 1),
Analysis I, II (Modul 2)
- Inhalt:
- Aufgabentypen; Elemente der konvexen Analysis und
Dualität; notwendige und hinreichende
Optimalitätsbedingungen, Regularität, Existenz von
Lösungen; klassische Aufgaben; Standard-Lösungsmethoden
1. und 2. Ordnung; zentrale analytische Hilfsmittel für
Extremalprobleme in
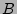 -Räumen (Trennung, Dualität,
Sätze von Lyusternik und Ekeland).
-Räumen (Trennung, Dualität,
Sätze von Lyusternik und Ekeland).
- Übungen:
- 2 SWS pro Woche:
Di 13-15 Uhr, RUD 25, 3.011; B. Kummer
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.408, Tel. 2093-5844
(32459)
MATHEMATISCHE STATISTIK (D-AN,A) R. THRUM
4 SWS VL pro Woche, Di 13-15 Uhr, RUD 25, 4.007; Do 13-15 Uhr,
RUD 25, 3.006
- Inhalt:
- Entscheidungstheoretische Grundlagen; Schlußweisen,
Methoden und Anwendungen der Mathematischen Statistik;
Konstruktionsprinzipien und Eigenschaften von
Parameterschätzungen; Prüfen von Hypothesen;
Neymann-Pearson-Theorie, Exponentialfamilien.
- Übungen:
- 2 SWS pro Woche:
Di 15-17 Uhr, RUD 25, 4.007; R. Thrum
- Literatur:
- Lehmann: Theory of Point Estimation & Testing Stat.
Hypothesis.
Witting, H.: Math. Statistik I.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.207, Tel. 2093-5838
(32460)
NICHTPARAMETRISCHE METHODEN
UND IHRE ANWENDUNGEN
(D-AN,A) V. SPOKOINYI
2 SWS VL pro Woche, Di 13-15 Uhr, ZI 13A
(32462)
L´EVY-PROZESSE UND
STOCHASTISCHE DIFFERENTIALGLEICHUNGEN
(D-AN,A) I. PAVLYUKEVICH
2 SWS VL pro Woche, Mo 15-17 Uhr, RUD 25, 1.115
- Voraussetzungen:
- Elemente von Stochastik II und Stochastischer Analysis
- Inhalt:
- Lévy-Prozesse, stochastische Integration, Itô-Formel,
stochastische Differentialgleichungen.
- Literatur:
- Applebaum, D.: Lévy processes and stochastic calculus.
Cambridge University Press, 2004.
Protter, P.E.: Stochastic integration and differential
equations. Springer, 2004.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.208, Tel. 2093-5845
(32463)
STOCHASTIK II (D-AN,A) P. IMKELLER
4 SWS VL pro Woche, Mo 09-11 Uhr, RUD 26, 1'304; Di 09-11 Uhr,
RUD 26, 1'304
- Voraussetzungen:
- Lineare Algebra und Analytische Geometrie I, II (Modul
1), Analysis I, II (Modul 2), Maßtheorie (Teilmodul 6a),
Stochastik I (Modul 8)
- Inhalt:
- Bedingte Erwartungen, Martingale in diskreter Zeit:
Stopp- und Konvergenzsätze mit Anwendungen, Konstruktion
stochastischer Prozesse, Markov-Ketten, schwache
Konvergenz von Maßen, Invarianzprinzip und Brownsche
Bewegung.
- Übungen:
- 2 SWS pro Woche:
Di 11-13 Uhr, RUD 25, 4.007; D. Peithmann
- Literatur:
- Wird noch bekanntgegeben.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.218, Tel. 2093-5850
(32464)
EINFÜHRUNG IN DIE
STOCHASTISCHE FINANZMATHEMATIK
(D-AN,A) J. SCHOENMAKERS
4 SWS VL pro Woche, Mo 13-15 Uhr, RUD 26, 1'304; Fr 09-11 Uhr,
RUD 26, 1'304
- Voraussetzungen:
- Lineare Algebra und Analytische Geometrie I, II (Modul
1), Analysis I, II (Modul 2), Maßtheorie (Teilmodul 6a),
Stochastik I (Modul 8), empfohlen wird außerdem der
(evtl. parallele) Besuch der Vorlesung Stochastik II
(Modul 24).
- Inhalt:
- Einführung in zeitlich diskrete stochastische
Finanzmarktmodelle und die entsprechenden
martingaltheoretischen und funktionalanalytischen
Methoden: Arbitragefreiheit und Martingalmaße,
Finanzderivate und ihre Bewertung, Black-Scholes-Formel,
effiziente Absicherungsstrategien, Risikomaße, optimales
Stoppen und amerikanische Optionen.
- Übung:
- 2 SWS pro Woche:
Fr 11-13 Uhr, RUD 25, 3.007; I. Penner
(32465)
RISIKOTHEORIE (VERSICHERUNGSMATHEMATIK II) (D-AN,A) M. RIEDLE
2 SWS VL pro Woche, Do 09-11 Uhr, RUD 25, 3.006
- Voraussetzungen:
- Stochastik I
- Inhalt:
- Stochastische Modelle für Risiken bei Versicherungen und
auf Finanzmärkten. Im Mittelpunkt stehen u.a.
Gesamtschadenverteilungen im Rahmen individueller und
kollektiver Modelle, Extremwerttheorie, Risikoprozesse,
Ruinwahrscheinlichkeiten, Prämienkalkulationsprinzipien,
Peak-over-Threshold-Methode, Value-at-Risk und kohärente
Risikomaße.
Die Vorlesung ist für Studierende der Studienrichtung
Diplommathematiker vorgesehen und kann für die
Nebenfachausbildung ,,Wirtschaftswissenschaften``
anerkannt werden. Sie wird außerdem den Studierenden des
Masterstudienganges Statistik angeboten. Auch weitere
Interessenten sind willkommen.
Von der Deutschen Aktuarvereinigung e.V. wird die
erfolgreiche Teilnahme an der Lehrveranstaltung
(inklusive mündlicher Prüfung) als Prüfung im Fach
,,Schadenversicherungsmathematik`` anerkannt (s.
www.aktuar.de).
- Übungen:
- 1 SWS pro Woche:
Do 11-13 Uhr, 14tgl. (1. Woche), RUD 25, 2.009; M. Riedle
- Literatur:
- Embrechts, P.; Klüppelberg, C.; Mikosch, T.: Modelling
Extremal Events. Springer, 1997.
Mack, T.: Schriftenreihe Angew. Versicherungsmathematik:
Schadenversicherungsmathematik. 2000.
Rolski, T.; Schmidli, H.; Schmidt, V.; Tengels, J.:
Stochastic processes for insurance and finance.
Weitere Literatur wird in der Vorlesung angegeben.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.210, Tel. 2093-5874
(32468)
EINFÜHRUNG IN DIE
MATHEMATISCHE LOGIK
(D-RE,R; L-VII) A. BAUDISCH
4 SWS VL pro Woche, Mo 09-11 Uhr, RUD 25, 1.115; Mi 09-11 Uhr,
RUD 26, 1'304
- Inhalt:
- Es werden grundlegende Begriffe der mathematischen Logik
eingeführt, wobei der Prädikatenkalkül erster Stufe im
Mittelpunkt steht. Höhepunkte der Vorlesung sind die
Gödelschen Sätze.
- Übungen:
- 2 SWS pro Woche:
Mi 11-13 Uhr, RUD 26, 1'304; A. Baudisch
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.403, 2093-5824
(32472)
ALGEBRA/ZAHLENTHEORIE (L-IV) R.-P. HOLZAPFEL
4 SWS VL pro Woche, Mo 11-13 Uhr, RUD 25, 1.115; Mi 13-15 Uhr,
RUD 26, 1'304
- Voraussetzungen:
- Grundstudium
- Inhalt:
- Peano-Axiome, ganze, rationale, reelle und komplexe
Zahlen, einfache diophantische Gleichungen, Geometrie in
der komplexen Zahlenebene, euklidische Ringe,
Kongruenzen, Anwendung in der Codierungstheorie
(CD-Brenn-Code).
- Übungen:
- 2 SWS pro Woche:
Mi 15-17 Uhr, RUD 26, 1'304; R.-P. Holzapfel
- Literatur:
- Ebbinghaus u.a.: Zahlen.
- Geplante Fortsetzung:
- SS 2007, 2 SWS VL und 2 SWS SE
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.427, Tel. 2093-1439
(32473)
NUMERISCHE MATHEMATIK (L-VI) H.-D. NIEPAGE
4 SWS VL pro Woche, Mo 15-17 Uhr, RUD 26, 1'304; Di 09-11 Uhr,
RUD 25, 1.115
- Inhalt:
- Lösungsmethoden für lineare Gleichungssysteme
(Eliminations- und Iterationsverfahren),
Iterationsmethoden für nichtlineare Gleichungen,
Interpolation von Funktionen, numerische Integration,
Fehleranalyse. Vorlesung und Übung (mit
Praktikumsanteilen) orientieren sich an der
schulpraktischen Relevanz der Themen und dem sinnvollen
Computereinsatz im Mathematik-Unterricht.
- Übungen:
- 2 SWS pro Woche:
Di 11-13 Uhr, RUD 26, 1'304; H.-D. Niepage
- Geplante Fortsetzung:
- SS 2007, Vorlesung: Vertiefungskurs Numerische Mathematik
(Lehramt, 2 SWS), Seminar: Ausgewählte Kapitel der
Numerischen Mathematik (2 SWS)
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.022, Tel. 2093-5868
hpt 2006-11-02