32428
BMS BASIC COURSE ,,COMMUTATIVE ALGEBRA`` -
ALGEBRA II
(D-RE,R) [10 SP] J. KRAMER
4 SWS VL pro Woche, Do 11-13 Uhr, RUD 26, 1'304; Do 15-17 Uhr,
RUD 26, 1'304
- Voraussetzungen:
- Lineare Algebra und Analytische Geometrie I, II, Algebra
I
- Inhalt:
- Noethersche Ringe, faktorielle Ringe, Polynomringe;
Moduln; Elemente der homologischen und multilinearen
Algebra; Algebren über Körpern (z.B. halbeinfache und
einfache Matrix-Algebren).
- Übung:
- 2 SWS pro Woche, Mi 09-11 Uhr, RUD 25, 1.011; O. Teschke
- Sprechstunden:
- Mittwoch, 15-16 Uhr, RUD 25, 2.303, Tel. 2093-5815
32430
KOHOMOLOGIE-THEORIEN UND IHRE ANWENDUNGEN (D-RE,R) W. KLEINERT
4 SWS VL pro Woche, Mo 11-13 Uhr, RUD 26, 0'311; Fr 13-15 Uhr,
RUD 25, 1.013
- Voraussetzungen:
- Moduln Algebra II, Topologie sowie kommutative Algebra
und/oder Algebraische Geometrie I. Diese Voraussetzungen
sind nützlich, aber nicht unabdingbar.
- Inhalt:
- Kategorien, Funktoren und Grundlagen der homologischen
Algebra; derivierte Kategorien und derivierte Funktoren;
Garben und Garben-Kohomologietheorien;
Grothendieck-Topologien und Stacks; Gruppen-Kohomologie;
Anwendungen in der algebraischen, arithmetischen und
komplex-analytischen Geometrie, Spektralsequenzen;
charakteristische Klassen.
- Übung:
- 2 SWS pro Woche, Mo 13-15 Uhr, RUD 25, 1.012; W. Kleinert
- Literatur:
- [1] Kashiwara, M.; Schapira, P.: Categories and Sheaves.
Springer, 2006.
[2] Iversen, B.: Cohomology of Sheaves. Springer, 1986.
[3] Gelfand, S.I.; Manin, Yu.I.: Methods of Homological
Algebra. Springer, 1996.
- Geplante Fortsetzung:
- z.Z. keine
- Sprechstunden:
- Mittwoch, 14-16 Uhr, RUD 25, 1.426, Tel. 2093-1435
32431
ALGEBRAIC CURVES AND RIEMANN SURFACES (D-RE,R) G. FARKAS
4 SWS VL pro Woche, Di 13-15 Uhr, RUD 25, 1.115; Mi 09-11 Uhr,
RUD 26, 0'311
- Voraussetzungen:
- Familiarity with the theory of complex functions. Basic
knowledge of manifolds and algebra is also desirable but
is not a requirement.
- Inhalt:
- This course will offer a gentle introduction to algebraic
geometry by the study of the algebraic curves over the
complex numbers (compact Riemann surfaces). Topics to be
treated will include Abel's theorem and the Jacobian
variety of a Riemann surface, the Riemann-Roch theorem
and the study of linear systems, an introduction to
sheaves in the context of algebraic curves, theta
functions.
- Übung:
- 2 SWS pro Woche, Mi 11-13 Uhr, RUD 25, 1.115; G. Farkas
- Literatur:
- Miranda, R.: Algebraic curves and Riemann surfaces.
Graduate Studies in Mathematics 5, American Mathematical
Society, 1995.
Forster, O.: Lectures on Riemann surfaces. Springer
Graduate Texts in Mathematics. Vol. 81, 1999.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.401, Tel. 2093-5412
32432
LOKALE KÖRPER (D-RE,R) E. GROßE-KLÖNNE
4 SWS VL pro Woche, Mo 15-17 Uhr, RUD 25, 1.114; Mi 13-15 Uhr,
RUD 25, 1.114
- Voraussetzungen:
- Algebra I
- Inhalt:
- Für eine fixierte Primzahl
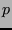 studieren wir den Körper
studieren wir den Körper 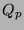 der
der 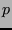 -adischen Zahlen, oder allgemeiner: eine
endliche Körpererweiterung
-adischen Zahlen, oder allgemeiner: eine
endliche Körpererweiterung 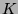 von
von 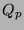 (man nennt
(man nennt 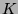 einen lokalen Körper). Von
großem Interesse für die algebraische Zahlentheorie
(ebenso: die Arithmetik von Modulformen, die Geometrie
arithmetischer Varietäten) ist das Verständnis der
absoluten Galoisgruppe von
einen lokalen Körper). Von
großem Interesse für die algebraische Zahlentheorie
(ebenso: die Arithmetik von Modulformen, die Geometrie
arithmetischer Varietäten) ist das Verständnis der
absoluten Galoisgruppe von 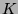 bzw. ihrer Darstellungstheorie.
Wir geben eine elementare Einführung.
bzw. ihrer Darstellungstheorie.
Wir geben eine elementare Einführung.
32433 fällt aus
KOHOMOLOGIE VON GRUPPEN UND ANWENDUNGEN (D-RE,R) V. HEIERMANN
2 SWS VL pro Woche, Mo 09-11 Uhr, RUD 25, 1.114
32434
TOPOLOGIE (D-RE,R)
[10 SP] TH. FRIEDRICH
4 SWS VL pro Woche, Di 11-13 Uhr, RUD 25, 1.013; Fr 09-11 Uhr,
RUD 26, 1'304
- Voraussetzungen:
- Modul 1, 2 und 7
- Inhalt:
- Grundbegriffe der mengentheoretischen Topologie,
Homotopieklassen, Homotopiegruppen, singuläre Homologie
und Kohomologie.
- Übung:
- 2 SWS pro Woche, Fr 11-13 Uhr, RUD 25, 3.007; Th.
Friedrich
- Sprechstunden:
- Dienstag, 08-09 Uhr, RUD 25, 1.301, Tel. 2093-1628
32435
BMS BASIC COURSE ,,FUNCTIONAL ANALYSIS`` -
HÖHERE ANALYSIS I (FUNKTIONALANALYSIS)
(D-RE,R,AN,A) [10 SP] J. SPREKELS
4 SWS VL pro Woche, Do 09-11 Uhr, RUD 25, 1.013; Do 13-15 Uhr,
RUD 25, 1.013
- Voraussetzungen:
- Anfängerausbildung in Analysis und Linearer Algebra
- Inhalt:
- Normierte Räume, Hilbert-Räume, Sätze von Hahn-Banach
und Banach-Steinhaus, schwache und schwach-
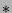 -Konvergenz,
open mapping theorem, Reflexivität, Sobolev-Räume,
Minimierung und Variationsungleichungen, Spektraltheorie
kompakter Operatoren, Satz von Schauder,
Differenzierbarkeit in normierten Räumen.
-Konvergenz,
open mapping theorem, Reflexivität, Sobolev-Räume,
Minimierung und Variationsungleichungen, Spektraltheorie
kompakter Operatoren, Satz von Schauder,
Differenzierbarkeit in normierten Räumen.
- Übung:
- 2 SWS pro Woche, Di 11-13 Uhr, RUD 26, 0'307; J. Heerda
- Literatur:
- Wird in der Vorlesung bekanntgegeben; es wird ein
Skriptum herausgegeben.
- Geplante Fortsetzung:
- SS 2008 BMS basic course ,,Partial Differential
Equations`` - Höhere Mathematik II (Partielle
Differentialgleichungen) (4 SWS VL + 2 SWS UE)
- Sprechstunden:
- Donnerstag, 12-13 Uhr, RUD 25, 2.105, Tel. 2093-5437
32436
BMS BASIC COURSE ,,COMPLEXE ANALYSIS`` -
KOMPLEXE ANALYSIS (D-RE,R;L) W. GUBLER
4 SWS VL pro Woche, Mo 13-15 Uhr, RUD 25, 4.007,Mo 15-17 Uhr, RUD
25, 4.007
Inhalt:
Im ersten Halbsemester wird die klassische Funktionentheorie
in einer Veränderlichen behandelt bis zum Residuensatz. Dies ist
äquivalent zum Teilmodul 6b. Im zweiten Halbsemester wird eine
Einführung in Nevanlinna Theorie gegeben.
- Übung:
- 2 SWS pro Woche, Mo 17-19 Uhr, RUD 25, 4.007; W. Gubler
32437
Beginn 22.10.2007
DIE -METHODE IN
KOMPLEXER ANALYSIS UND KOMPLEXER GEOMETRIE (D-RE,R) J. LEITERER
4 SWS VL pro Woche, Mo 13-15 Uhr, RUD 25, 3.011; Mi 13-15 Uhr,
RUD 25, 3.011
- Voraussetzungen:
- Grundkenntnisse über holomorphe Funktionen mehrerer
Veränderlicher sowie die Integrationstheorie auf
Mannigfaltigkeiten (Differentialformen, Satz von Stokes)
- Inhalt:
- Die
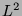 -Methode als Verfahren zur Lösung der
folgenden Aufgaben: Beweis der Verschwindungssätze auf
streng pseudokonvexen Mannigfaltigkeiten, Beweis einer
Reihe von Endlichkeitssätzen, Beweis des
Einbettungssatzes von Kodaira.
-Methode als Verfahren zur Lösung der
folgenden Aufgaben: Beweis der Verschwindungssätze auf
streng pseudokonvexen Mannigfaltigkeiten, Beweis einer
Reihe von Endlichkeitssätzen, Beweis des
Einbettungssatzes von Kodaira.
- Übung:
- 2 SWS pro Woche, Mo 15-17 Uhr, RUD 25, 3.011; J. Leiterer
- Literatur:
- Demailly, J.-P.: Complex analytic and algebraic geometry.
(Existiert nur im Netz auf der Seite von Demailly).
Huybrechts, D.: Complex geometry. Springer, 2005.
- Sprechstunden:
- Freitag, 13-14 Uhr, RUD 25, 1.420, 2093-1807
32438
BMS BASIC COURSE ,,ANALYSIS AND GEOMETRY ON MANIFOLDS``
-
ANALYSIS UND GEOMETRIE AUF MANNIGFALTIGKEITEN (D-RE,R) [10 SP] D.
SCHÜTH
4 SWS VL pro Woche, Di 13-15 Uhr, RUD 26, 1'304; Mi 15-17 Uhr,
RUD 25, 1.013
- Voraussetzungen:
- Modul 1 ,,Lineare Algebra und Analytische Geometrie I,
II``, Modul 2 ,,Analysis I, II``, Modul 5 ,,Analysis
IIIa`` und Modul 6 ,,Analysis IIIb``, wobei es genügt,
das Modul 5 parallel zu hören.
-
- http://www.math.hu-berlin.de/~schueth/agmws07.html
-
- Inhalt:
- Differenzierbare Mannigfaltigkeiten, Differentialformen,
Satz von Stokes, Einführung in die Riemannsche
Geometrie. Diese Vorlesung ist Voraussetzung für
Differentialgeometrie I.
- Übung:
- 2 SWS pro Woche, Mi 13-15 Uhr, RUD 26, 1'304; P. Schemel
- Literatur:
- DoCarmo, M.: Riemannian Geometry. Birkhäuser.
O'Neill, B.: Semi-Riemannian Geometry. Academic Press.
Warner, F.: Foundations of Differentiable Manifolds and
Lie Groups. Springer.
- Geplante Fortsetzung:
- Differentialgeometrie I (4 VL + 2 UE)
- Sprechstunden:
- Sprechstunde Mo 15 -16 Uhr, RUD 25, 1.316, Tel. 2093-5864
32442
GEOMETRIC STRUCTURES ON
(NILPOTENT & SOLVABLE) LIE GROUPS (D-RE,R) S. CHIOSSI, R. CLEYTON
2 SWS VL pro Woche, Do 09-11 Uhr, RUD 25, 1.012
- Voraussetzungen:
- Vordiplom, Differentialgeometrie I, Vorkenntnisse auf dem
Gebiet der Lie-Gruppen und der Darstellungstheorie sind
nützlich, aber nicht zwingend erforderlich.
- Inhalt:
- Nilpotent and solvable Lie groups, geometric structures,
compact quotients, special geometry, examples in dim 4 -
8, deformation theory, Einstein metrics and a conjecture
of Alekseevskii.
- Literatur:
- Wird in der Vorlesung angegeben (keine entsprechenden
Lehrbücher).
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.409, Tel. 2093-5407 (S.
Chiossi); RUD 25, 1.318, Tel. 2093-1818 (R. Cleyton)
32444
EINFÜHRUNG IN DIE
GEOMETRISCHE MAßTHEORIE (D-RE,R,AN,A) J. NAUMANN
2 SWS VL pro Woche, Mo 09-11 Uhr, RUD 25, 2.009
- Voraussetzungen:
- Analysis IIIb (Maß- u. Integrationstheorie), Höhere
Analysis I (Funktionalanalysis)
- Inhalt:
- Signierte Maße, Funktionen beschränkter Variation,
Minimum-Probleme für Funktionale mit linearem Wachstum,
Raum BD (Funktionen beschränkter Deformation).
- Literatur:
- http://www.math.hu-berlin.de/
 jnaumann/web/literatur/main-de.htm
jnaumann/web/literatur/main-de.htm
- Geplante Fortsetzung:
- keine
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.114, Tel. 2093-2239
32445
SOBOLEV-RÄUME (D-RE,R,AN,A) J. NAUMANN
2 SWS VL pro Woche, Mo 13-15 Uhr, RUD 25, 2.009
- Voraussetzungen:
- Analysis IIIb (Maß- u. Integrationstheorie), Höhere
Analysis I (Funktionalanalysis)
- Inhalt:
- Begriff der schwachen Ableitung, Raum
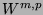 ,
Eigenschaften der Elemente aus
,
Eigenschaften der Elemente aus 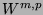 ,
Einbettungssätze.
,
Einbettungssätze.
- Literatur:
- http://www.math.hu-berlin.de/
 jnaumann/web/literatur/main-de.htm
jnaumann/web/literatur/main-de.htm
- Geplante Fortsetzung:
- keine
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.114, Tel. 2093-2239
32447
fällt aus
NICHTLINEARE PARTIELLE DIFFERENTIALGLEICHUNGEN
(D-RE,R,AN,A) J. NAUMANN
2 SWS VL pro Woche, Di 09-11 Uhr, RUD 25, 2.009
- Voraussetzungen:
- Analysis IIIb, Höhere Analysis I, Sobolev-Räume
- Inhalt:
- Kompakte Operatoren, Fixpunktsatz von Schauder,
Gleichungen mit monotonen Operatoren, Anwendung:
nichtlineare elliptische Randwert-Probleme,
Variationsmethoden und konvexe Funktionale,
Galerkin-Methode für nichtlineare parabolische Probleme.
- Literatur:
- http://www.math.hu-berlin.de/
 jnaumann/web/literatur/main-de.htm
jnaumann/web/literatur/main-de.htm
- Geplante Fortsetzung:
- keine
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.114, Tel. 2093-2239
32448
NICHTLINEARE FUNKTIONALANALYSIS
(D-RE,R,AN,A) J. NAUMANN
4 SWS VL pro Woche, Do 15-17 Uhr, RUD 25, 3.011; Fr 13-15 Uhr,
RUD 25, 3.011
- Voraussetzungen:
- Analysis I, II, IIIa,b; Höhere Analysis I
- Inhalt:
- Fixpunktsätze von Brouwer und Schauder, Methode von
Leray-Schauder, Gleichungen mit monotonen Operatoren,
Variationsmethoden und konvexe Funktionale, nichtlineare
Evolutionsgleichungen.
- Literatur:
- http://www.math.hu-berlin.de/
 jnaumann/web/literatur/main-de.htm
jnaumann/web/literatur/main-de.htm
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.114, Tel. 2093-2239
32449
MONOTONE OPERATOREN UND ANWENDUNGEN (D-RE,R,AN,A) L. RECKE
4 SWS VL pro Woche, Mi 11-13 Uhr, RUD 25, 1.114; Do 09-11 Uhr,
RUD 25, 2.009
- Voraussetzungen:
- Höhere Analysis I und II
- Inhalt:
- Stark monotone, Lipschitz-stetige Operatoren. Monotone,
koerzive, hemistetige Operatoren (Satz von Browder und
Minty). Maximale Monotonie (Satz von Browder).
Pseudomonotonie (Satz von Brezis).
Approximationsschemata. Anwendungen auf quasilineare
elliptische, parabolische und hyperbolische partielle
Differentialgleichungen und auf Variationsungleichungen.
- Literatur:
- Zeidler, E.: Nonlinear Functional Analysis and its
Applications. Vol II/A and II/B: Linear and Nonlinear
Monotone Operators. Springer, 1990.
- Sprechstunden:
- Montag, 14-15 Uhr, RUD 25, 2.112, Tel. 2093-2282
32451
FUNKTIONENRÄUME FÜR
NICHTGLATTE PARABOLISCHE PROBLEME (D-RE,R,AN,A) J.A. GRIEPENTROG
2 SWS VL pro Woche, Di 15-17 Uhr, RUD 25, 3.008
- Voraussetzungen:
- Grundstudium Analysis I, II, IIIa, IIIb,
Funktionalanalysis
- Inhalt:
- Parabolische Randwertprobleme zweiter Ordnung mit
nichtglatten Daten, Morrey- und Campanato-Räume,
Poincaré-Ungleichungen, Mengen mit Lipschitz-Rand,
Sobolev-Morrey-Räume für Evolutionsgleichungen nebst
Einbettungs- und Spursätzen.
- Geplante Fortsetzung:
- SS 2008, Regularitätstheorie für nichtglatte
parabolische Probleme
- Sprechstunden:
- nach Vereinbarung, Tel. 20372551
32452
EINFÜHRUNG IN DIE KONTROLLTHEORIE (D-AN,A) A. GLITZKY
2 SWS VL pro Woche, Fr 11-13 Uhr, RUD 25, 1.012
- Voraussetzungen:
- Analysis I, II, IIIa,b, gewöhnliche
Differentialgleichungen
- Inhalt:
- In der VL werden einfache Steuerungsprobleme für
gewöhnliche Differentialgleichungen vorgestellt, an
ihnen die wichtigsten Grundbegriffe der Kontrolltheorie
erklärt und typische Fragestellungen motiviert.
Anschließend werden wichtige Resultate aus der linearen
Kontrolltheorie bewiesen. Wesentlicher Inhalt der VL sind
Aussagen zur Beobachtbarkeit, zur Steuerbarkeit
(Nullsteuerbarkeit, ohne und mit Kontrollrestriktionen),
zum Realisierungs- und Identifizierbarkeitsproblem für
lineare Kontrollsysteme. Zusätzlich werden verschiedene
Arten von Optimalsteuerungsproblemen vorgestellt. Für
zeitoptimale Steuerungsprobleme wird ein Existenzsatz,
ein Kriterium für Extremalität und ein Maximumprinzip
bewiesen.
- Sprechstunden:
- nach Vereinbarung, WIAS, Tel. 20372-568
42453
FUNCTION SPACE
OPTIMIZATION (D-AN,A) A. GRIEWANK
3 SWS VL pro Woche, Mi 15-17 Uhr, RUD 26, 0'311; Do 11-13 Uhr,
14tgl. (1. Woche), RUD 25, 1.115
- Voraussetzungen:
- Higher Analysis (Functional Analysis), Basic nonlinear
optimization course
- Inhalt:
- Optimality conditions in Hilbert and Banach Spaces,
convergence properties of gradient and Newton methods,
linear invariance and Mesh Independence Results.
- Übung:
- 1 SWS pro Woche, Do 11-13 Uhr, 14tgl. (2. Woche), RUD 25,
1.115; A. Griewank
- Literatur:
- Jahn, J.: Introduction to the Theory of Nonlinear
Optimization.
Ponstein, J.: Approaches to the theory of optimization.
Gehrenberger, P.: Optimization by vector space methods.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.426, Tel. 2093-5820
32455
OPTIMIERUNGSPROBLEME
MIT WAHRSCHEINLICHKEITSRESTRIKTIONEN
(D-AN,A) R. HENRION
2 SWS VL pro Woche, Fr 09-11 Uhr, RUD 25, 3.011
- Voraussetzungen:
- Modul 1 und 2
- Inhalt:
- Optimierungsprobleme mit Zufallsparametern, Modelle,
Struktur (Stetigkeit, Differenzierbarkeit, Konvexität),
Numerik, Anwendung auf Praxisprobleme.
- Sprechstunden:
- nach Vereinbarung, WIAS
32456
NUMERIK PARTIELLER DIFFERENTIALGLEICHUNGEN I (D-AN,A) [10 SP] A.
SCHRÖDER
4 SWS VL pro Woche, Mo 15-17 Uhr, RUD 26, 0'311; Do 09-11 Uhr,
RUD 26, 1'304
- Inhalt:
- Klassische Lösungen und Differenzenverfahren für
elliptische und parabolische Differentialgleichungen,
elliptische Variationsgleichungen, Galerkin-Verfahren,
Methode der finiten Elemente, Fehlerabschätzung, Finite
Volumen Methode, Apriori- und
Aposteriori-Fehlerschätzer.
- Übung:
- 2 SWS pro Woche, Do 11-13 Uhr, RUD 25, 3.008; N.N.
- Praktikum:
- 2 SWS pro Woche, Do 13-15 Uhr, RUD 25, 2.207; N.N. (fak.)
32457
NUMERIK GEWÖHNLICHER
DIFFERENTIALGLEICHUNGEN
(D-AN,A) [8 SP] W. RÖMISCH
4 SWS VL pro Woche, Di 13-15 Uhr, RUD 25, 1.013; Fr 11-13 Uhr,
RUD 25, 1.013
- Voraussetzungen:
- Grundvorlesung Numerische Mathematik
- Inhalt:
- Existenz und Stabilität von Lösungen gewöhnlicher
Differentialgleichungen, Elemente der Diskretisierung von
Operatorgleichungen, Integrationsverfahren für
Anfangswertprobleme, Stabilität, Konsistenz, Konvergenz,
asymptotisches Verhalten, Schieß- und
Kollokationsverfahren für Randwertaufgaben.
- Literatur:
- Strehmel; Weiner: Numerik gewöhnlicher
Differentialgleichungen. Teubner.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.414, Tel. 2093-2561
32459
THEORIE UND VERFAHREN
DER NICHTGLATTEN OPTIMIERUNG
(D-RE,R,AN,A) B. KUMMER
4 SWS VL pro Woche, Mo 15-17 Uhr, RUD 25, 1.115; Mi 13-15 Uhr,
RUD 25, 1.115
- Voraussetzungen:
- Analysis I, II, Algebra I
- Inhalt:
- Nichtglatte Optimierungsaufgaben entstehen vor allem
dann, wenn Lösungen gegebener Aufgaben in weiteren
Problemen auftreten (hierarchische, multiphase oder
multilevel Probleme). Dann sind in der Regel die für
klassische Zugänge nötigen
Differenzierbarkeits-Voraussetzungen nicht erfüllt, was
für Optimalitätsbedingungen und Verfahren wesentlich
ist und (ca. seit 1980) zur Entwicklung der sogenannten
nichtglatten Optimierung (und - Analyis) führte. Die VL
soll eine Einführung in dieses Gebiet geben, zentrale
Begriffe, Sätze und Herangehensweisen vorstellen und
einen Einblick in Anwendungen und den aktuellen Stand der
Forschung vermitteln. Zum andern sollen die Verbindungen
zur klassischen Theorie und mögliche Grenzen aufgezeigt
werden.
Stichworte: Subdifferentiale, Variationsprinzipien,
verallgemeinerte Ableitungen, stabile Lösungen,
Lipschitz Funktionen, mehrwertige Abbildungen,
nichtglatte Newton-Verfahren, Komplementarität und
NCP-Funktionen.
- Literatur:
- (Monographien)
- Clarke, F.H.: Optimization and Nonsmooth
Analysis. Wiley, 1983.
- Hiriart-Urruty, J.-B.; Lemarechal, C.: Convex
Analysis and Minimization Algorithms I, II.
Springer, 1993.
- Outrata, J.; Kocvara, M.; Zowe, J.: Nonsmooth
Approach to Optimization Problems with
Equilibrium Constraints. Kluwer, 1998.
- Rockafellar, R.T.; Wets, R.J.-B.: Variational
Analysis. Springer 1998.
- Bonnans, J.F.; Shapiro, A.: Perturbation Analysis
of Optimization Problems. Springer, 2000.
- Klatte, D.; Kummer, B.: Nonsmooth Equations in
Optimization. Kluwer, 2002.
- Facchinei, F.; Pang, J.-S.: Finite-Dimensional
Variational Inequalities and Complementary
Problems, I, II. Springer, 2003.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.408, Tel. 2093-5844
32460
EINFÜHRUNG IN DIE SPIELTHEORIE (D-AN,A) B. KUMMER
4 SWS VL pro Woche, Mo 11-13 Uhr, RUD 25, 1.115; Fr 13-15 Uhr,
RUD 26, 1'304
- Voraussetzungen:
- Analysis I, II, Algebra I
- Inhalt:
- Die VL stellt wichtige Klassen von Spielen und
Marktmodellen mit entsprechenden Lösungsbegriffen vor.
Schwerpunkte sind die Existenz und Konstruktion von
Lösungen für kooperative und nichtkooperative Modelle
wie Nash-Gleichgewicht, Edgeworth-, Walras-,
Verhandlungslösungen (Nash), Drohstabilität, von
Neumann-Morgenstern-Lösung, Shapley-Vektor und Core,
zusammen mit ihren Grundlagen: Fixpunktsätze von Brouwer
und Kakutani, Michaels selection theorem, spezielle
Aussagen aus der Optimierung. Daneben werden Lösungen in
Spielen mit vollständiger Information und die Struktur
von Nash-Lösungsmengen untersucht.
- Literatur:
- von Neumann, J.; Morgenstern, O.: Theory of Games
and Economic Behavior. Princeton, Univ. Press,
1944 (in deutsch u.a. Würzburg 1961).
- Rauhut, B.; Schmitz, N.; Zachow, E.-W.:
Spieltheorie. Teubner, Studienbücher Mathematik,
Stuttgart 1979.
- Kummer, B.: Spiele auf Graphen. Dt. Verlag der
Wiss., Berlin 1979, Birkhäuser 1980, Mir (russ.)
1982.
- Vorobiev, N.N.: Foundations of Game Theory -
Noncooperative Games. (in Russian), Nauka, Moscow
1984.
- Maskin, E.S.: Recent Developments in Game Theory.
Edward Elgar Publishing, Northhampton 1999.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.408, Tel. 2093-5844
32461
STOCHASTISCHE OPTIMIERUNG (D-AN,A) W. RÖMISCH
2 SWS VL pro Woche, Mo 13-15 Uhr, RUD 26, 1'304
- Voraussetzungen:
- Optimierung I, Stochastik I
- Inhalt:
- Angewandte Optimierungsprobleme unter Ungewissheit,
zweistufige und mehrstufige stochastische
Optimierungsprobleme, Optimalität und Dualität,
Approximation und Numerik.
- Literatur:
- Ruszczynski, A.; Shapiro, A. (eds.): Stochastic
Programming. Elsevier, 2003.
Wallace, S.W.; Ziemba, W.T. (eds.): Applications of
Stochastic Programming. SIAM-MPS, 2005.
- Sprechstunden:
- Mittwoch, 13-15 Uhr, RUD 25, 2.414, Tel. 2093-2561
32462
MATHEMATISCHE STATISTIK (D-AN,A) [10 SP] R. THRUM
4 SWS VL pro Woche, Mi 15-17 Uhr, RUD 26, 1'304; Fr 11-13 Uhr,
RUD 25, 1.115
- Inhalt:
- Entscheidungstheoretische Grundlagen; Schlußweisen,
Methoden und Anwendungen der Mathematischen Statistik;
Konstruktionsprinzipien und Eigenschaften von
Parameterschätzungen; Prüfen von Hypothesen;
Neymann-Pearson-Theorie, Exponentialfamilien.
- Übung:
- 2 SWS pro Woche, Fr 13-15 Uhr, RUD 25, 1.011; R. Thrum
- Literatur:
- Lehmann: Theory of Point Estimation & Testing Stat.
Hypothesis.
Witting, H.: Math. Statistik I.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.207, Tel. 2093-5838
32463
NICHTPARAMETRISCHE METHODEN
UND IHRE ANWENDUNGEN
(D-AN,A) V. SPOKOINY
2 SWS VL pro Woche, Fr 13-15 Uhr, RUD 25, 1.012
- Inhalt:
- Modern nonparametrics: Basics of the parametric theory;
local parametric approach; LMS, LCP and SSA procedure;
''oracle'' inequalities.
- Seminar:
- 2 SWS pro Woche, Fr 15-17 Uhr, RUD 25, 1.011; V. Spokoiny
32464
BMS BASIC COURSE ,,STOCHASTIC PROCESSES`` -
STOCHASTIK II
(D-AN,A) U. KÜCHLER
4 SWS VL pro Woche, Do 11-13 Uhr, RUD 25, 1.013; Do 15-17 Uhr,
RUD 25, 1.115
- Voraussetzungen:
- Stochastik I
- Inhalt:
- Conditional Expectations, continuous time processes,
Lévy processes (independent stationary increments),
Gaussian processes (Wiener process, fractional Brownian
motion), Martingales, Markov chains, applications in
Mathematical Finance, Biology and other fields.
- Übung:
- 2 SWS pro Woche, Mi 13-15 Uhr, RUD 25, 3.008; I. Penner.
- Literatur:
- Gighman, I.L., Skohorod, A.V.: Theory of Stochastic
Processes I-III. Springer-Verlag, 1974, 1975, 1979.
Weitere Literatur wird in der Vorlesung angegeben.
- Sprechstunden:
- Mittwoch, 13-15 Uhr, RUD 25, 1.202, Tel. 2093-5811
32465
EINFÜHRUNG IN DIE
STOCHASTISCHE FINANZMATHEMATIK
(D-AN,A) [10 SP] U. HORST
4 SWS VL pro Woche, Mi 09-11 Uhr, RUD 25, 1.115; Fr 09-11 Uhr,
RUD 25, 1.115
- Voraussetzungen:
- Lineare Algebra und Analytische Geometrie I, II (Modul
1), Analysis I, II (Modul 2), Maßtheorie (Teilmodul 6a),
Stochastik I (Modul 8), empfohlen wird außerdem der
(evtl. parallele) Besuch der Vorlesung Stochastik II
(Modul 24).
- Inhalt:
- Einführung in zeitlich diskrete stochastische
Finanzmarktmodelle und die entsprechenden
martingaltheoretischen und funktionalanalytischen
Methoden: Arbitragefreiheit und Martingalmaße,
Finanzderivate und ihre Bewertung, Black-Scholes-Formel,
effiziente Absicherungsstrategien, Risikomaße, optimales
Stoppen und amerikanische Optionen.
- Übung:
- 2 SWS pro Woche, Do 13-15 Uhr, RUD 25, 3.006; I. Penner.
32466
RISIKOTHEORIE (SCHADENSVERSICHERUNGSMATHEMATIK)
(D-AN,A) U. KÜCHLER
2 SWS VL pro Woche, Di 09-11 Uhr, RUD 25, 4.007
- Voraussetzungen:
- Stochastik I
- Inhalt:
- Stochastische Modelle für Risiken bei Versicherungen und
auf Finanzmärkten. Im Mittelpunkt stehen u.a.
Gesamtschadensverteilungen im Rahmen individueller und
kollektiver Modelle, Prämienkalkulationsprinzipien,
Ruinwahrscheinlichkeiten, Peak-over-Threshold-Methode,
Value-at-Risk und kohärente Risikomaße, Elemente der
Extremwerttheorie.
- Übung:
- 1 SWS pro Woche, Di 11-13 Uhr, 14tgl. (1. Woche), RUD 25,
4.007; U. Küchler
- Literatur:
- Embrechts, P.; Klüppelberg, C.; Mikosch, T.: Modelling
Extremal Events. Springer, 1997.
Hipp, C.; Michel, R.: Risikotheorie: Stochastische
Modelle und Statistische Methoden. Karlsruhe 1990.
Weitere Literatur wird in der Vorlesung angegeben.
- Sprechstunden:
- Mittwoch, 13-15 Uhr, RUD 25, 1.202, Tel. 2093-5811
32467 entfällt siehe als Ersatz unter zusätzlichen
Lehrveranstaltung VL H. Gilsing
MARKOV PROZESSE UND IHRE ANWENDUNGEN (D-AN,A) M. RIEDLE
2 SWS VL pro Woche, Di 13-15 Uhr, RUD 25, 2.009
- Voraussetzungen:
- Stochastik I, Stochastik II kann parallel gehört werden.
- Inhalt:
- Markov-Prozesse bilden eine in Theorie und Praxis weit
verbreitete Klasse von stochastischen Prozessen, zu denen
u.a. Poisson-Prozesse, Wiener-Prozesse, Geburts- und
Todesprozesse sowie Lévy-Prozesse gehören. In vielen
Bereichen, z.B. in der Versicherungs- und
Finanzmathematik sowie in den Naturwissenschaften, dienen
Markov-Prozesse zur Modellierung von zeitabhängigen,
zufälligen Erscheinungen.
In dieser VL wird die Theorie der Markov-Prozesse
vermittelt, z.B. Übergangshalbgruppen und ihre Erzeuger,
Fellereigenschaft, Stationarität, Ergodensätze. Diese
Ergebnisse werden zur Modellierung verschiedener
Beispiele in den oben genannten Bereichen genutzt, z.B.
PKW-Haftpflichtversicherung, Warteschlangen im
Supermarkt.
- Übung:
- 2 SWS pro Woche, Di 15-17 Uhr, RUD 25, 2.009; M. Riedle
- Literatur:
- Es wird ein Script zur VL herausgegeben.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.210, Tel. 2093-5874
32468 fällt aus
MONTE-CARLO-METHODEN FÜR SDES
MIT ANWENDUNGEN IN
DER FINANZMATHEMATIK
(D-AN,A) E. BUCKWAR
2 SWS VL pro Woche, Mo 11-13 Uhr, RUD 25, 1.114
- Inhalt:
- Schwache Approximationen von stochastischen
Differentialgleichungen, Varianzreduktionsmethoden,
Anwendungen in der Preisberechnung von Finanzderivaten.
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.217, Tel. 2093-5889
32471
EINFÜHRUNG IN DIE
MATHEMATISCHE LOGIK
(D-RE,R; L-VII) [10 SP] A. BAUDISCH
4 SWS VL pro Woche, Mo 09-11 Uhr, RUD 25, 1.115; Mi 11-13 Uhr,
RUD 26, 0'311
- Inhalt:
- Es werden grundlegende Begriffe der mathematischen Logik
eingeführt, wobei die elementare Logik im Mittelpunkt
steht. Höhepunkte der Vorlesung sind die Gödelschen
Sätze.
- Übungen:
- 2 SWS pro Woche, Mi 13-15 Uhr, RUD 25, 3.007; A. Baudisch
- Sprechstunden:
- nach Vereinbarung, RUD 25, 1.403, 2093-5824
32474
NUMERISCHE MATHEMATIK (L-VI) H.-D. NIEPAGE
4 SWS VL pro Woche, Di 09-11 Uhr, RUD 25, 1.115; Mi 09-11 Uhr,
RUD 25, 3.008
- Inhalt:
- Lösungsmethoden für lineare Gleichungssysteme
(Eliminations- und Iterationsverfahren),
Iterationsmethoden für nichtlineare Gleichungen,
Interpolation von Funktionen, numerische Integration,
Fehleranalyse. Vorlesung und Übung (mit
Praktikumsanteilen) orientieren sich an der
schulpraktischen Relevanz der Themen und dem sinnvollen
Computereinsatz im Mathematik-Unterricht.
- Übungen:
- 2 SWS pro Woche, Di 11-13 Uhr, RUD 25, 3.008; H.-D.
Niepage
- Sprechstunden:
- nach Vereinbarung, RUD 25, 2.022, Tel. 2093-5868
32475
ANALYSIS II (MA) [10 SP] D. SCHÜTH
4 SWS VL pro Woche, Mo 11-13 Uhr, RUD 26, 1'304, Mi 11-13 Uhr,
RUD 26, 1'304
- Voraussetzungen:
- Analysis I
- Inhalt:
- Vertiefung und Anwendung der Kenntnisse in Analysis,
Erlernen von mathematischen Schlußweisen und
Beweisstrategien, sprachlich-logische Schulung.
- Integration. Riemann-Integral (einer
reellen Variablen), Trapezregel, Hauptsatz der
Differential- und Integralrechnung.
- Differentialrechnung mehrerer
Veränderlicher. Stetigkeit, partielle,
totale und stetige Differenzierbarkeit, Satz
über die Umkehrfunktion, Satz über implizite
Funktionen im
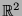 .
.
- Ausblick auf die Integralrechnung für
Funktionen mehrerer reeller Variablen.
Riemann-Integral, Berechnung von
Mehrfachintegralen, Volumen von
Rotationskörpern.
- Gewöhnliche Differentialgleichungen.
Grundlegende Begriffe, elementar lösbare
Differentialgleichungen.
http://www.math.hu-berlin.de/~schueth/an2ws07.html
- Übung:
- 2 SWS pro Woche, Mo 13-15 Uhr, RUD 25, 3.007; D. Schüth
- Literatur:
- Forster: Analysis. Band 1 und 2. Vieweg.
Barner, Flohr: Analysis. Band I und II. de Gruyter.
- Sprechstunden:
- Sprechstunde Mo 15 -16 Uhr, RUD 25, 1.316, Tel. 2093-5864
32476
DIDAKTIK DER MATHEMATIK IN DER SEKUNDARSTUFE II (MA) W. SCHULZ
2 SWS VL pro Woche, Mi 13-15 Uhr, RUD 26, 0'311
- Sprechstunden:
- Montag, 11-13 Uhr, RUD 25, 2.301, Tel. 2093-5870
hpt 2007-11-12