Wintersemester 2023/24
Office hours / further discussion: after the seminar or by appointment
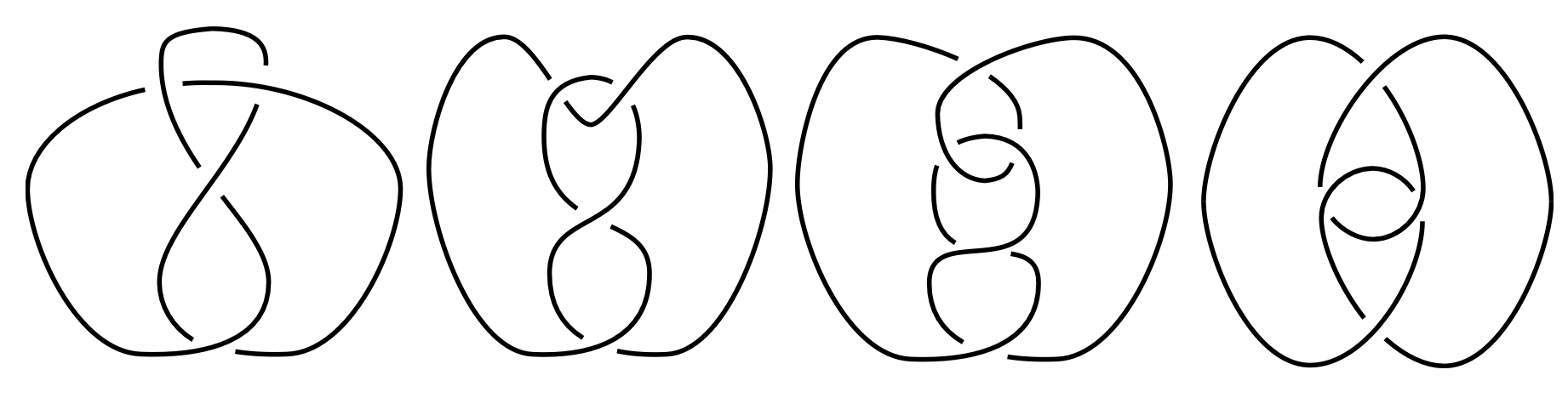
| 19.10.23 | Preliminary meeting and overview [P, Chapter 0] Marc Kegel |
||||||
| 23.11.23 | The figure-8 knot complement [P, Chapter 1] Cosima Schmitt |
||||||
| 30.11.23 14:00-15:30 |
Calculations in hyperbolic space [P, Chapter 2] Johannes Manstein |
||||||
| 7.12.23 |
no seminar |
||||||
| 14.12.23 | Hyperbolic structures on manifolds and triangulations [P, Chapter 3 and 4] Marc Kegel |
||||||
| [P] | J. Purcell,
Hyperbolic Knot Theory, 2020, available online on the arXiv:2002.12652. | ||||||