PDAEs with Uncertainties for the Analysis, Simulation and Optimization of Energy Networks
The project aims to provide a new theoretical framework for solving open questions in the control and design of energy networks regarding uncertainty. Subject of investigations are stochastic partial differential-algebraic equations studied as stochastic perator differential-algebraic equations and stochastic optimization problems subject to coupled dynamic and static constraints.
Project Heads
Caren Tischendorf, Nicolas Perkowski, René Henrion
Project Members
Project Webpage
Topic and Background
The project aims to support decision making for the design and control of energy networks like power networks or gas transport networks or couplings of them. Particular focus of the investigations are the uncertainties caused by fluctuations in demand and supply. Neglecting uncertainties, the transient behaviour of such networks can be described by systems of partial differential equations (e.g. the Euler equations for gas networks) coupled via algebraic constraints. A well-established approach for analyzing such systems is the formulation as an operator DAE of the form
A*(Dv(t))' + B(v(t)) = r(t), t∈ I
with linear operators A*: Z*→ V*, D: V → Z and a nonlinear operator B: V → V*, where I is a time interval and V, Z, H are Banach spaces such that Z ⊂ H ≡ H* ⊂ Z* forms an evolution triple. To include uncertainties in the demand and supply, the function r on the right-hand side shall be modeled as a stochastic process Rt which leads to a stochastic operator DAE of the form
A*d(DVt) + B(Vt) = C(t,Vt)dRt, t∈ I.
The first challenge for the existence of solutions is the proper choice of the stochastic process Rt. Existence of solutions is not guaranteed if we allow Rt to be a Wiener process because the algebraic part needs a proper treatment. As long as the system does not contain hidden constraints, an appropriate choice for Rt would be the use of an integrated diffusion, say an integrated mean-reverting Ornstein-Uhlenbeck process, for the algebraic part and the Wiener process for the differential part. This needs a separation of both parts which can be treated by a decoupling approach.
A second direction of research will add the optimization aspect to the consideration of PDAEs under uncertainty. The latter is assumed to be given as before by stochastic loads in the nodes of the network, however in the simpler setting of a random vector ξ (for instance, after a KarhunenLoève expansion of the original stochastic process). The decision u to be optimized could represent a certain design variable. The aim is to find optimal decisions which are robust in a probabilistic sense with respect to later actions of the random parameter. This results in the formulation of an optimization problem subject to a probabilistic constraint:
min f(u): A*(Dv(t))' + B(v(t)) = r(ξ, t), (t ∈ I), ℙ[g(u, v, ξ, t)≤ 0 ∀t ∈ I] ≥ p
In this model, a decision u is declared to be feasible whenever the probability of satisfying the infinite stochastic inequality system g(u, v, ξ, t) ≤ 0 ∀t ∈ I is satisfied with a probability larger than a specified level p ∈ (0, 1). The inequalities might represent, for instance, pressure bounds in a gas network. Probabilistic constraints represent a major model within stochastic optimization which is widely applied in engineering sciences, first of all in power management. Traditionally, they are considered in the framework of operations research, i.e., of finite-dimensional optimization.
Goals of the Project and Methodologies
A first goal will be to obtain a (possibly local) solution theory for the considered equations. For that purpose we will first study monotone parabolic SPDAEs and we will extend existing work on coupled systems to the stochastic setting. By extending the analysis to "locally monotone" coefficients, we hope to treat interacting networks of Navier-Stokes equations. Networks of Euler equations could then be derived in the vanishing viscosity limit. Additionally, we aim to exploit the port-Hamiltonian structure of the network equations for the construction of proper numerical schemes. In order to address the optimization problem, we plan to start with the question of feasibibility of solutions. On one hand we want to exploit ideas of the perturbation analysis that allows us to develop sufficient criteria for the validity of the inequality constraints for transient solutions. On the other hand, we intend to incorporate for the first time probabilistic constraints (moreover of implicit type) into optimization problems subject to uncertain PDAEs. asdf
Current Work
For our first direction of research, “Monotone SPDEs with Algebraic Constraints”, we consider coupled systems of the form
dx(t) + f(t,x,y,z)dt – R(t,x,y,z)dWtR = 0, (SDE)
g(t,x,y,z) = 0, (AE)
dz(t) - A(t,x,y,z)dt – B(t,x,y,z)dWtB = 0, (SPDE)
consisting of a stochastic differential equation (SDE), an algebraic constraint (AE) and a stochastic partial differential equation (SPDE). This special semi-explicit scheme empowers the decoupling approach and naturally resembles the structure arising in circuit and gas network simulation. Using this ansatz, we obtain existence and uniqueness results.
In the second direction of research, “Optimization Problems with Probabilistic Constraints”, we developed an optimization scheme for (currently) small gas networks, using the spheric-radial decomposition (SRD). Our numerical experiments produce in this case promising results compared to Monte Carlo (MC) and Quasi-Monte Carlo (QMC) methods.
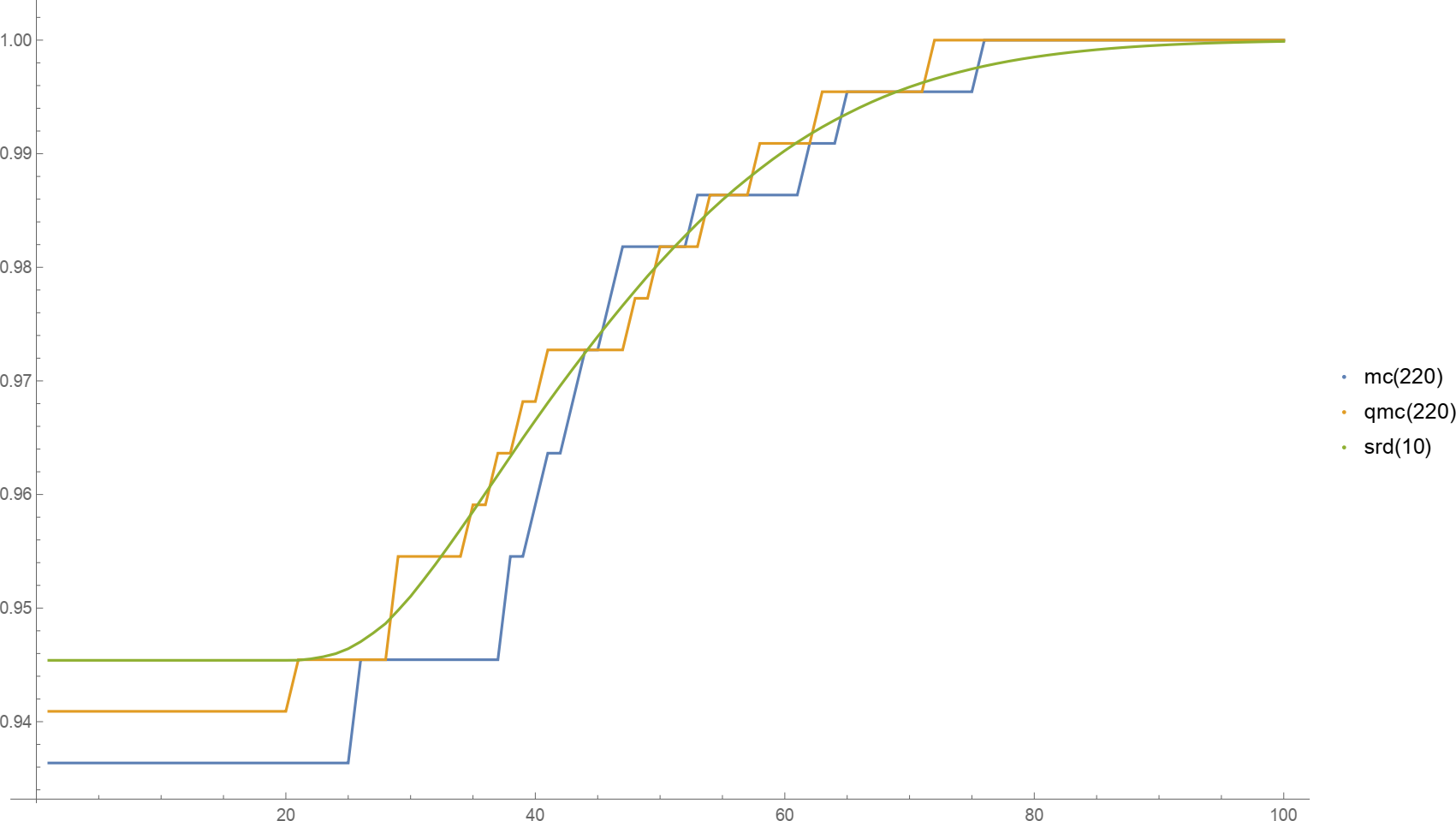
Plots of the probability function for MC, QMC and SRD with respective number of samples
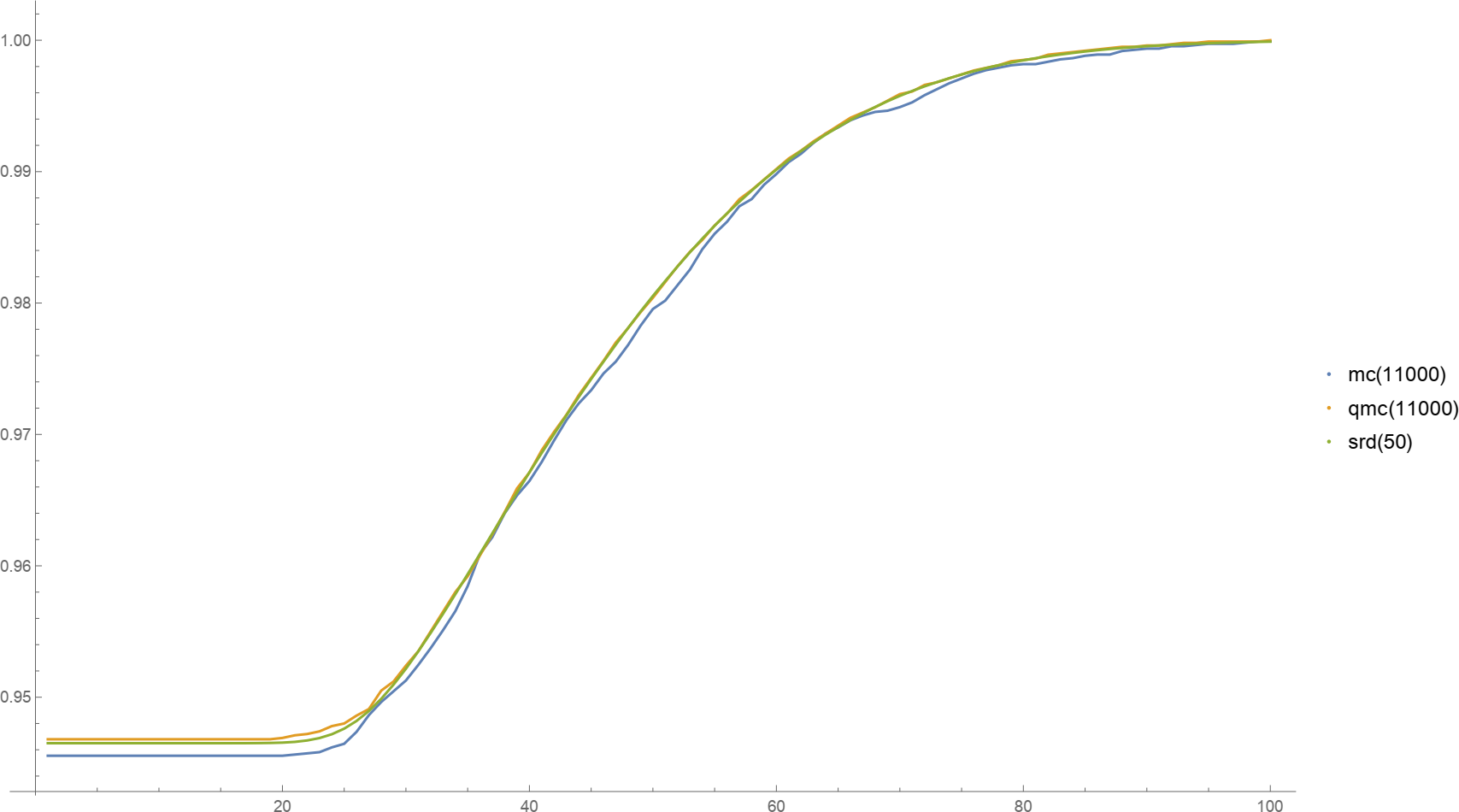
Plots of the probability function for MC, QMC and SRD with respective number of samples
In contrast to the Monte Carlo and Quasi-Monte Carlo methods, the SRD method produces a smooth approximation. Accordingly, each step is more costly to compute, e.g., 10 SRD sample points compare to 220 MC or QMC samples in computation time. However, in this case the SRD method did not improve after 50 samples and MC/QMC seem to converge to this ‘limit’. This indicates that SRD produces quicker good results by having a faster convergence.
