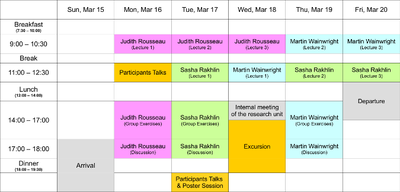
Schedule
The program consists of three lecture series (4.5 hours each) plus associated exercise sessions, a poster session, and short-talks given by the participants.
Lectures
The lectures (including exercise sessions) will be given by
-
Martin Wainwright (UC Berkeley)
-> Download slides
-> Download exercises
Non-parametric estimation: Non-asymptotic guarantees and high-dimensional scaling -
Sasha Rakhlin (University of Pennsylvania)
-> Download slides
-> Download exercises
From Statistical to Online Learning We will start with the problems of statistical learning and
estimation, and show that empirical processes play a key role in
analyzing the minimax performance. We will then make a natural
transition to the online learning world. After building a toolbox of
"sequential" analogues of empirical process theory, we will analyze
online regression and other online learning problems. A relaxation
framework, based on approximate dynamic programming, will provide a
general approach to developing computationally attractive prediction
methods. Many examples will be discussed, along with future
directions. -
Judith Rousseau (Université Paris-Dauphine)
-> Download slides
-> Download exercises
Lectures on non-parametric Bayes Some of the topics to be covered are:
- posterior consistency in Bayesian large dimensional models
- empirical Bayes
- posterior concentration rates: Bernstein von Mises
- frequentist coverage properties of Bayesian credible regions in large or infinite dimensional models
Poster Session
There will be a poster session. All participants are strongly encouraged to contribute a poster (vertical A0 format preferred, but you may deviate from this).
Participants Short Introduction
All participants should give a mini presentation in order to briefly introduce themselves and their research interests within 2-3 minutes, supported by one or at most two slides. Please send your slide(s) until March 11 as a single .pdf-file to sven.kurras@uni-hamburg.de.